Cara Mencari Luas dan Volume Bola Panduan Lengkap

Bola, bentuk geometris yang sederhana namun elegan, menyimpan misteri matematika yang menarik. Dari bola sepak hingga planet-planet di tata surya, pemahaman tentang luas permukaan dan volume bola sangat krusial. Menguasai perhitungan ini membuka pintu menuju pemahaman yang lebih dalam tentang dunia di sekitar kita, mulai dari desain arsitektur hingga perhitungan ilmiah yang kompleks. Artikel ini akan menjadi panduan praktis untuk menguasai perhitungan luas permukaan dan volume bola, dilengkapi contoh soal dan aplikasi nyata dalam kehidupan sehari-hari.

Kita akan menjelajahi rumus-rumus kunci, langkah-langkah perhitungan yang sistematis, serta aplikasi praktisnya dalam berbagai bidang. Dengan pemahaman yang komprehensif, Anda akan mampu menyelesaikan berbagai permasalahan yang melibatkan bola, baik itu soal ujian maupun permasalahan di dunia nyata. Siap untuk menyelami dunia geometri bola?

Rumus Luas Permukaan Bola

Menghitung luas permukaan bola merupakan konsep dasar dalam geometri yang memiliki aplikasi luas dalam berbagai bidang, mulai dari perencanaan konstruksi hingga pengembangan produk. Memahami rumus dan aplikasinya sangat penting untuk memecahkan berbagai masalah terkait ukuran dan volume objek berbentuk bola.

Rumus luas permukaan bola didasarkan pada jari-jari bola tersebut. Pemahaman yang mendalam tentang rumus ini memungkinkan kita untuk menghitung luas permukaan berbagai objek sferis dengan akurat.

Rumus Luas Permukaan Bola dan Variabelnya

Luas permukaan bola dihitung menggunakan rumus:

L = 4πr²

Jelaskan Cara Melakukan Passing Bawah Bola Voli

di mana:

• L = Luas permukaan bola
• r = Jari-jari bola
• π (pi) ≈ 3.14159

Rumus ini menunjukkan bahwa luas permukaan bola berbanding lurus dengan kuadrat jari-jarinya. Semakin besar jari-jari bola, semakin besar pula luas permukaannya.

Contoh Perhitungan Luas Permukaan Bola dengan Jari-jari 5 cm

Berikut contoh perhitungan luas permukaan bola dengan jari-jari 5 cm, disajikan dalam :

Jari-jari (r)	Rumus	Perhitungan	Hasil (cm²)
5 cm	L = 4πr²	L = 4 × 3.14159 × (5 cm)²	314.159 cm²

Langkah-langkah Perhitungan Luas Permukaan Bola dengan Jari-jari 10 cm

Mari kita uraikan langkah-langkah perhitungan luas permukaan bola dengan jari-jari 10 cm:

1. Tentukan jari-jari: Jari-jari bola adalah 10 cm.
2. Substitusikan ke rumus: Gunakan rumus L = 4πr², substitusikan nilai r = 10 cm.
3. Hitung kuadrat jari-jari: 10 cm × 10 cm = 100 cm²
4. Kalikan dengan 4π: 4 × 3.14159 × 100 cm² ≈ 1256.636 cm²
5. Hasil: Luas permukaan bola dengan jari-jari 10 cm adalah sekitar 1256.636 cm².

Contoh Soal Cerita dan Penyelesaiannya

Sebuah balon udara berbentuk bola memiliki jari-jari 7 meter. Berapa luas permukaan balon udara tersebut?

1. Identifikasi variabel: Jari-jari (r) = 7 meter
2. Gunakan rumus: L = 4πr²
3. Substitusikan dan hitung: L = 4 × 3.14159 × (7 m)² ≈ 615.75 m²
4. Kesimpulan: Luas permukaan balon udara tersebut sekitar 615.75 meter persegi.

Perbandingan Rumus Luas Permukaan Bola dengan Bangun Ruang Lainnya

Berikut perbandingan rumus luas permukaan bola dengan bangun ruang lain:

• Bola: L = 4πr² (bergantung pada jari-jari)
• Kubus: L = 6s² (bergantung pada panjang sisi)
• Tabung: L = 2πr² + 2πrh (bergantung pada jari-jari dan tinggi)

Perbedaan rumus ini mencerminkan perbedaan bentuk dan karakteristik geometri masing-masing bangun ruang. Rumus bola hanya bergantung pada jari-jari, sedangkan kubus dan tabung melibatkan lebih dari satu variabel.

Rumus Volume Bola

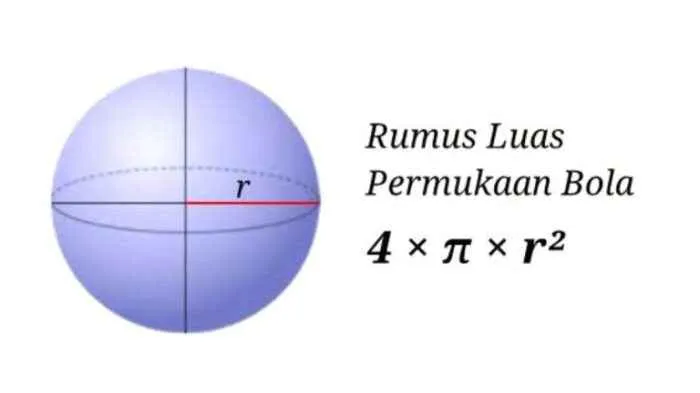
Menghitung volume bola merupakan hal fundamental dalam berbagai bidang, mulai dari teknik sipil hingga fisika. Memahami rumusnya dan penerapannya sangat penting untuk menyelesaikan berbagai permasalahan yang melibatkan bentuk bola. Berikut penjelasan detail mengenai rumus volume bola dan contoh penerapannya.

Rumus dan Variabel Volume Bola

Rumus volume bola dinyatakan sebagai:

V = (4/3)πr³

di mana:

• V = Volume bola
• r = Jari-jari bola
• π (pi) ≈ 3,14159

Rumus ini menunjukkan bahwa volume bola berbanding lurus dengan pangkat tiga jari-jarinya. Artinya, jika jari-jari bola digandakan, maka volumenya akan menjadi delapan kali lipat.

Contoh Perhitungan Volume Bola dengan Jari-jari 7 cm

Misal jari-jari bola (r) = 7 cm
Maka, volume bola (V) = (4/3) x π x 7³ cm³
V ≈ (4/3) x 3,14159 x 343 cm³
V ≈ 1436,755 cm³

Langkah Perhitungan Volume Bola dengan Diameter 14 cm

Jika diketahui diameter bola adalah 14 cm, maka jari-jari bola (r) adalah setengah dari diameter, yaitu 7 cm. Berikut langkah-langkah perhitungannya:

1. Tentukan jari-jari bola: r = 14 cm / 2 = 7 cm
2. Substitusikan nilai jari-jari ke dalam rumus volume bola: V = (4/3)πr³
3. Hitung volume bola: V = (4/3) x 3,14159 x 7³ cm³ = 1436,755 cm³

Jadi, volume bola dengan diameter 14 cm adalah sekitar 1436,755 cm³.

Contoh Soal Cerita dan Penyelesaiannya

Sebuah balon udara berbentuk bola memiliki diameter 10 meter. Berapa volume udara di dalam balon tersebut?

1. Tentukan jari-jari bola: r = 10 m / 2 = 5 m
2. Substitusikan nilai jari-jari ke dalam rumus volume bola: V = (4/3)πr³
3. Hitung volume bola: V = (4/3) x 3,14159 x 5³ m³ ≈ 523,6 m³

Jadi, volume udara di dalam balon tersebut sekitar 523,6 meter kubik.

Perbandingan Rumus Volume Bola dengan Bangun Ruang Lainnya

Berikut perbandingan rumus volume bola dengan bangun ruang lainnya, kubus dan tabung:

Bangun Ruang	Rumus Volume	Contoh Perhitungan (sisi/jari-jari = 5 satuan)	Kesimpulan Perbandingan
Bola	V = (4/3)πr³	V ≈ 523,6 satuan kubik	Volume bergantung pada pangkat tiga jari-jari.
Kubus	V = s³	V = 125 satuan kubik	Volume bergantung pada pangkat tiga sisi.
Tabung	V = πr²t	(dengan tinggi t = 10 satuan) V ≈ 785,4 satuan kubik	Volume bergantung pada pangkat dua jari-jari dan tinggi.

Penerapan Rumus Luas dan Volume Bola dalam Kehidupan Sehari-hari

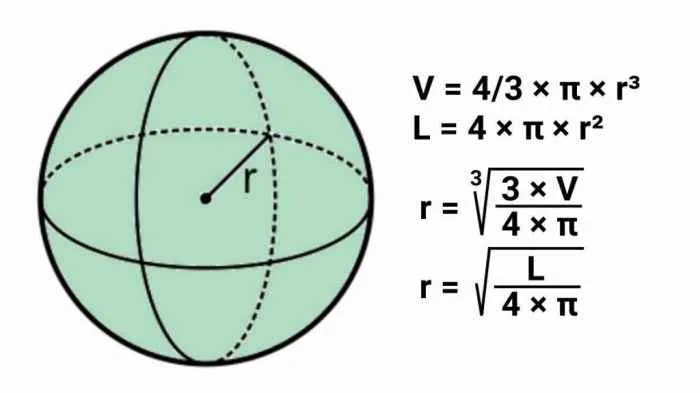
Rumus luas permukaan dan volume bola, meskipun terlihat sederhana, memiliki aplikasi luas dalam berbagai aspek kehidupan kita. Dari desain bola sepak hingga perhitungan kapasitas tangki penyimpanan, pemahaman konsep ini krusial. Berikut beberapa contoh penerapannya yang mungkin tak terpikirkan sebelumnya.

Penerapan Rumus Luas Permukaan Bola

Luas permukaan bola, yang dihitung dengan rumus 4πr², penting dalam menentukan kebutuhan material untuk berbagai objek berbentuk bola atau hampir bola.

• Desain Bola Sepak: Produsen bola sepak perlu menghitung luas permukaan bola untuk menentukan jumlah kulit yang dibutuhkan dalam proses pembuatan. Perhitungan ini memastikan efisiensi material dan kualitas produk. Ukuran bola sepak yang standar memiliki radius tertentu, sehingga perhitungan luas permukaannya menjadi kunci dalam proses produksi.
• Pelapisan Bola Logam: Dalam industri, pelapisan bola logam dengan cat atau bahan lain membutuhkan perhitungan luas permukaan yang akurat. Ini memastikan pemakaian bahan pelapis yang efisien dan hasil akhir yang merata. Misalnya, pada proses pelapisan bola baja untuk mencegah korosi, perhitungan luas permukaan sangat penting untuk menentukan jumlah bahan pelapis yang dibutuhkan.
• Desain Planetarium: Desain kubah planetarium yang berbentuk setengah bola (hemisfer) membutuhkan perhitungan luas permukaan untuk menentukan jumlah material yang diperlukan dalam pembangunannya. Perhitungan yang akurat akan meminimalisir pemborosan material dan memastikan konstruksi yang tepat.

Penerapan Rumus Volume Bola

Rumus volume bola, ⁴⁄₃πr³, penting dalam menentukan kapasitas penyimpanan atau jumlah material yang dibutuhkan untuk objek berbentuk bola.

• Kapasitas Tangki Penyimpanan: Tangki penyimpanan air atau bahan cair berbentuk bola sering digunakan karena efisiensi strukturnya. Perhitungan volume bola penting untuk menentukan kapasitas penyimpanan yang tepat. Misalnya, sebuah tangki penyimpanan air berbentuk bola dengan radius 5 meter akan memiliki kapasitas penyimpanan sebesar 523,6 liter (menggunakan pendekatan π ≈ 3,14).
• Produksi Bola Berongga: Dalam industri, pembuatan bola berongga seperti bola lampu atau bola mainan membutuhkan perhitungan volume untuk menentukan jumlah material yang dibutuhkan. Perhitungan ini juga penting untuk memastikan ketebalan dinding bola yang sesuai dengan fungsinya.
• Perhitungan Volume Sel Darah Merah: Dalam bidang biologi, perhitungan volume sel darah merah yang berbentuk hampir bola membantu dalam memahami karakteristik dan fungsi sel darah merah. Meskipun bentuknya tidak sempurna bola, pendekatan dengan rumus volume bola memberikan estimasi yang cukup akurat.

Tabel Perbandingan Penerapan Rumus Bola

Penerapan	Rumus yang Digunakan	Penjelasan	Contoh Numerik
Luas Permukaan Bola Sepak (r=11cm)	4πr²	Menentukan jumlah kulit yang dibutuhkan	4π(11cm)² ≈ 1520 cm²
Volume Tangki Penyimpanan Air (r=5m)	⁴⁄₃πr³	Menentukan kapasitas penyimpanan	⁴⁄₃π(5m)³ ≈ 523,6 m³
Volume Bola Berongga (r luar=10cm, r dalam=9cm)	⁴⁄₃π(r_luar³ – r_dalam³)	Menentukan jumlah material yang dibutuhkan	⁴⁄₃π(10³ – 9³) ≈ 113,1 cm³
Luas Permukaan Kubah Planetarium (r=20m) (setengah bola)	2πr²	Menentukan jumlah material untuk konstruksi	2π(20m)² ≈ 2513 m²

Penerapan dalam Teknik dan Sains

Rumus luas permukaan dan volume bola memiliki peran penting dalam berbagai bidang teknik dan sains. Dalam teknik sipil, perhitungan ini digunakan dalam desain struktur seperti kubah dan tangki penyimpanan. Dalam teknik mesin, perhitungan ini penting dalam desain komponen mesin yang berbentuk bola. Di bidang fisika, rumus ini digunakan dalam perhitungan gaya gravitasi, medan listrik, dan lainnya. Dalam ilmu kedokteran, pemahaman tentang volume bola membantu dalam memahami fisiologi dan patologi organ-organ tubuh.

Skenario Perhitungan Luas dan Volume Bola Secara Bersamaan

Sebuah perusahaan sedang merancang sebuah wahana berbentuk bola untuk wisata bawah laut. Wahana ini memiliki radius 2 meter dan terbuat dari bahan akrilik transparan. Perusahaan perlu menghitung luas permukaan akrilik yang dibutuhkan untuk membuat dinding wahana dan volume udara di dalam wahana untuk memastikan kenyamanan penumpang. Luas permukaan akrilik yang dibutuhkan adalah 4π(2m)² ≈ 50,27 m². Volume udara di dalam wahana adalah ⁴⁄₃π(2m)³ ≈ 33,51 m³. Perhitungan ini memastikan penggunaan material yang efisien dan kapasitas udara yang cukup untuk penumpang.

Menentukan Jari-jari Bola jika Diketahui Luas Permukaan atau Volume

Menentukan jari-jari bola merupakan langkah krusial dalam berbagai perhitungan geometri. Kemampuan ini dibutuhkan untuk menghitung luas permukaan dan volume bola secara akurat. Berikut ini langkah-langkah praktis untuk menentukan jari-jari bola jika diketahui luas permukaan atau volumenya.

Menentukan Jari-jari Bola jika Diketahui Luas Permukaan

Luas permukaan bola dirumuskan sebagai 4πr², di mana r adalah jari-jari bola. Untuk menentukan jari-jari, rumus ini perlu dibalik. Dengan demikian, jari-jari (r) dapat dicari dengan rumus r = √(Luas Permukaan / 4π).

1. Bagi luas permukaan bola dengan 4π.
2. Akar kuadratkan hasil bagi tersebut.
3. Hasilnya adalah jari-jari bola.

Contoh Soal dan Penyelesaian Menentukan Jari-jari dari Luas Permukaan

Misalkan luas permukaan bola adalah 100π cm². Maka, jari-jari bola dapat dihitung sebagai berikut:
r = √(100π cm² / 4π) = √(25 cm²) = 5 cm
Jadi, jari-jari bola adalah 5 cm.

Ilustrasi Penentuan Jari-jari Bola dari Luas Permukaan 100π cm²

Bayangkan sebuah bola dengan luas permukaan 100π cm². Kita tahu rumus luas permukaan bola adalah 4πr². Dengan mensubstitusikan nilai luas permukaan, kita peroleh persamaan 100π = 4πr². Dengan membagi kedua ruas dengan 4π, kita dapatkan r² = 25. Akar kuadrat dari 25 adalah 5, sehingga jari-jari bola tersebut adalah 5 cm. Visualisasikan bola tersebut dengan diameter 10 cm, yang membagi bola menjadi dua bagian yang sama.

Menentukan Jari-jari Bola jika Diketahui Volume

Volume bola dirumuskan sebagai (4/3)πr³. Untuk mencari jari-jari, rumus ini perlu dibalik. Dengan demikian, jari-jari (r) dapat dicari dengan rumus r = ³√(3V / 4π), di mana V adalah volume bola.

1. Kalikan volume bola dengan 3.
2. Bagi hasil kali tersebut dengan 4π.
3. Akar pangkat tiga hasil bagi tersebut.
4. Hasilnya adalah jari-jari bola.

Contoh Soal dan Penyelesaian Menentukan Jari-jari dari Volume

Misalkan volume bola adalah 36π/3 cm³. Maka, jari-jari bola dapat dihitung sebagai berikut:
r = ³√((3 * (36π/3 cm³)) / 4π) = ³√(36π cm³ / 4π) = ³√(9 cm³) = 3 cm
Jadi, jari-jari bola adalah 3 cm.

Ilustrasi Penentuan Jari-jari Bola dari Volume 36π/3 cm³

Perhatikan sebuah bola dengan volume 36π/3 cm³. Kita gunakan rumus volume bola (4/3)πr³. Substitusikan nilai volume, sehingga (4/3)πr³ = 36π/3. Sederhanakan persamaan menjadi r³ = 9. Akar pangkat tiga dari 9 adalah 3, sehingga jari-jari bola tersebut adalah 3 cm. Visualisasikan bola dengan diameter 6 cm, yang dapat dibagi menjadi dua bagian dengan luas penampang lingkaran yang sama.

Ringkasan Akhir

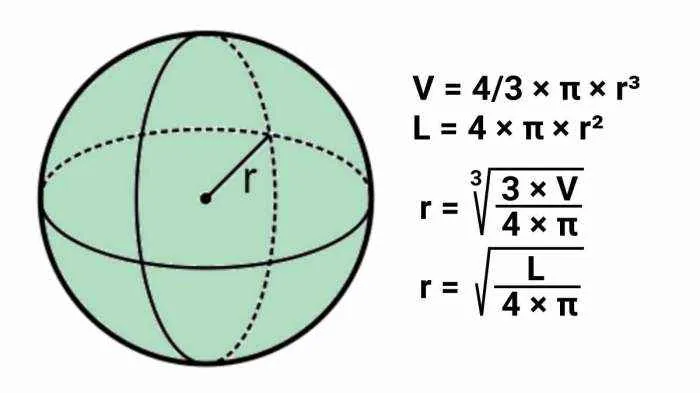
Menguasai perhitungan luas permukaan dan volume bola bukanlah sekadar latihan matematika; ini adalah kunci untuk memahami dan memecahkan berbagai permasalahan di dunia nyata. Dari mendesain stadion olahraga hingga menghitung volume cairan dalam tangki penyimpanan berbentuk bola, kemampuan ini memiliki aplikasi yang luas dan penting. Dengan pemahaman yang kuat terhadap konsep dan rumus yang telah dibahas, Anda kini memiliki alat yang ampuh untuk menghadapi tantangan perhitungan geometri yang lebih kompleks. Teruslah berlatih dan aplikasikan pengetahuan ini untuk membuka lebih banyak peluang di bidang ilmu pengetahuan dan teknologi.