Cara Mencari Luas Kulit Bola Panduan Lengkap

Sepak bola, bola basket, bahkan planet Bumi—semuanya memiliki bentuk bola. Mengetahui luas permukaan bola, atau luas kulit bola, penting dalam berbagai aplikasi, mulai dari perhitungan kebutuhan cat untuk lapangan bola hingga perkiraan luas permukaan planet. Rumus sederhana namun ampuh membuka pintu untuk memahami dunia tiga dimensi dengan lebih baik. Mari kita selami dunia geometri bola dan kuasai cara menghitung luas kulit bola.

Artikel ini akan memandu Anda langkah demi langkah dalam menghitung luas permukaan bola, mulai dari memahami rumus dasar hingga mengaplikasikannya dalam berbagai konteks kehidupan nyata. Kita akan membahas contoh-contoh perhitungan, menangani konversi satuan, dan mengidentifikasi potensi kesalahan umum yang perlu dihindari. Dengan pemahaman yang komprehensif ini, Anda akan siap untuk menghitung luas kulit bola dengan akurat dan percaya diri.

Rumus Luas Permukaan Bola

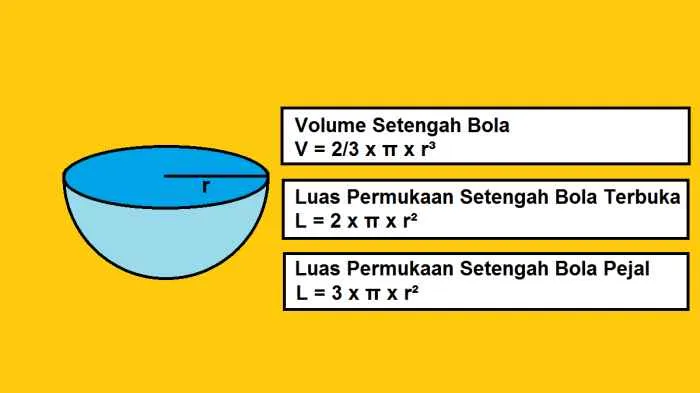
Menghitung luas permukaan bola merupakan konsep fundamental dalam geometri. Pemahaman tentang rumus ini penting dalam berbagai aplikasi, mulai dari perhitungan volume udara dalam balon hingga perencanaan proyek konstruksi yang melibatkan bentuk bola. Artikel ini akan menguraikan rumus luas permukaan bola, langkah-langkah perhitungannya, dan memberikan contoh penerapannya.

Rumus Luas Permukaan Bola dan Variabelnya

Luas permukaan bola dihitung menggunakan rumus 4πr², di mana:

4πr²

Variabel ‘r’ merepresentasikan jari-jari bola. π (pi) adalah konstanta matematika yang nilainya mendekati 3,14159. Rumus ini menunjukkan bahwa luas permukaan bola berbanding lurus dengan kuadrat jari-jarinya. Semakin besar jari-jari bola, semakin besar pula luas permukaannya.

Contoh Perhitungan Luas Permukaan Bola

Misalnya, kita ingin menghitung luas permukaan bola dengan jari-jari 5 cm. Dengan menggunakan rumus 4πr², kita substitusikan nilai r = 5 cm:

Luas permukaan = 4 × π × (5 cm)² = 4 × π × 25 cm² ≈ 314,16 cm²

Jadi, luas permukaan bola dengan jari-jari 5 cm adalah sekitar 314,16 cm².

Tabel Rumus, Variabel, dan Satuan

Rumus	Variabel	Satuan	Keterangan
4πr²	r (jari-jari)	cm, m, km, dst.	Jari-jari bola
	π (pi)	Konstanta	≈ 3.14159

Ilustrasi Penurunan Rumus dari Konsep Geometri Bola

Rumus luas permukaan bola dapat diilustrasikan melalui pendekatan integral. Bayangkan bola dipotong menjadi banyak sekali irisan tipis berbentuk lingkaran. Luas setiap irisan dapat dihitung dengan rumus luas lingkaran (πr²). Dengan menjumlahkan luas semua irisan tipis tersebut dan mengambil limit ketika ketebalan irisan mendekati nol, kita akan mendapatkan integral yang menghasilkan rumus 4πr².

Secara visual, dapat dibayangkan bahwa semakin banyak irisan lingkaran yang dibuat, semakin akurat pendekatan luas permukaan bola. Proses ini menunjukkan bagaimana rumus 4πr² merupakan representasi matematis dari penjumlahan luas semua elemen kecil yang membentuk permukaan bola.

Langkah-langkah Perhitungan Luas Permukaan Bola

1. Tentukan jari-jari (r) bola.
2. Kuadratkan jari-jari (r²).
3. Kalikan hasil kuadrat dengan 4π.
4. Hasil akhir adalah luas permukaan bola.

Penerapan Rumus Luas Permukaan Bola

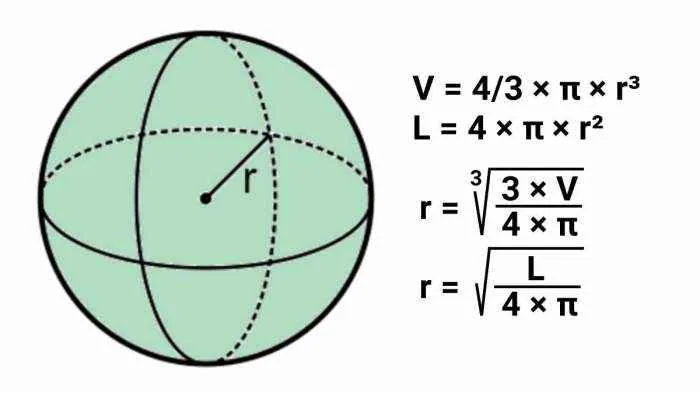
Rumus luas permukaan bola, 4πr², memiliki aplikasi luas di berbagai bidang, dari perhitungan sederhana sehari-hari hingga perencanaan proyek berskala besar. Memahami penerapan rumus ini memungkinkan kita untuk menyelesaikan berbagai permasalahan yang melibatkan bentuk bola, baik secara teoritis maupun praktis.

Contoh Penerapan Rumus Luas Permukaan Bola dalam Kehidupan Sehari-hari

Salah satu contoh penerapannya adalah menghitung kebutuhan cat untuk mengecat bola. Bayangkan Anda ingin mengecat sebuah bola dunia berdiameter 50 cm. Untuk mengetahui jumlah cat yang dibutuhkan, Anda perlu menghitung luas permukaan bola tersebut terlebih dahulu. Dengan mengetahui luas permukaan, Anda dapat memperkirakan jumlah cat yang diperlukan dengan mempertimbangkan daya sebar cat per satuan luas.

Perhitungan Luas Permukaan Bola dengan Diameter 10 cm

Mari kita hitung luas permukaan bola dengan diameter 10 cm. Langkah-langkahnya sebagai berikut:

1. Tentukan jari-jari (r): Diameter adalah 10 cm, jadi jari-jari (r) adalah 10 cm / 2 = 5 cm.
2. Gunakan rumus luas permukaan bola: Luas Permukaan = 4πr²
3. Substitusikan nilai jari-jari: Luas Permukaan = 4 * π * (5 cm)² = 100π cm²
4. Hitung nilai numerik (dengan menggunakan nilai π ≈ 3.14159): Luas Permukaan ≈ 314.159 cm²

Jadi, luas permukaan bola dengan diameter 10 cm adalah sekitar 314.159 cm².

Perbandingan Luas Permukaan Dua Bola dengan Jari-jari Berbeda

Berikut perbandingan luas permukaan dua bola dengan jari-jari berbeda. Tabel ini menunjukkan bagaimana perubahan jari-jari secara signifikan memengaruhi luas permukaan bola.

Jari-jari (cm)	Luas Permukaan (cm²)	Perhitungan	Perbandingan Luas
5	314.16	4π(5)²	1
10	1256.64	4π(10)²	4

Penggunaan Rumus Luas Permukaan Bola pada Berbagai Jenis Bola

Rumus luas permukaan bola berlaku untuk semua jenis bola, terlepas dari material atau ukurannya. Baik bola sepak, bola basket, atau bola biliar, rumus yang sama digunakan untuk menghitung luas permukaannya. Perbedaannya hanya terletak pada nilai jari-jari masing-masing bola.

Contoh Soal Cerita dan Penyelesaiannya

Sebuah perusahaan manufaktur bola voli ingin melapisi bola voli mereka dengan lapisan pelindung. Jika setiap bola voli memiliki diameter 21 cm, dan perusahaan memproduksi 1000 bola voli, berapa luas total lapisan pelindung yang dibutuhkan?

1. Tentukan jari-jari (r): Jari-jari bola voli adalah 21 cm / 2 = 10.5 cm.
2. Hitung luas permukaan satu bola voli: Luas Permukaan = 4π(10.5 cm)² ≈ 1385.44 cm²
3. Hitung luas total lapisan pelindung untuk 1000 bola voli: 1385.44 cm²/bola * 1000 bola ≈ 1.385.440 cm²

Jadi, perusahaan membutuhkan sekitar 1.385.440 cm² lapisan pelindung.

Menentukan Jari-jari Bola dari Luas Permukaannya

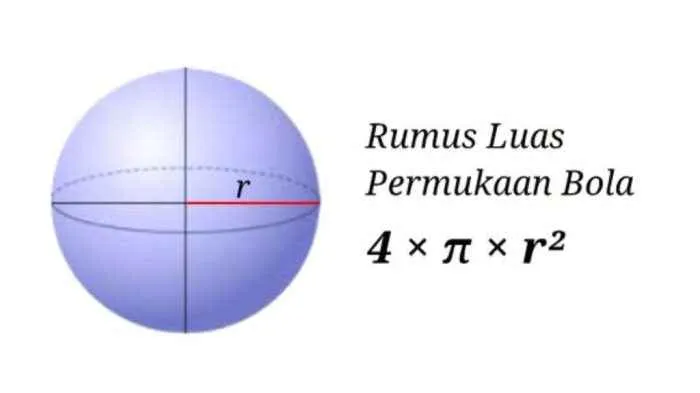
Menghitung luas permukaan bola relatif mudah, namun bagaimana jika kita hanya mengetahui luas permukaannya dan ingin mencari jari-jari bola tersebut? Kemampuan untuk menentukan jari-jari dari luas permukaan memiliki aplikasi praktis di berbagai bidang, mulai dari desain kemasan hingga perencanaan proyek konstruksi yang melibatkan bentuk bola. Berikut uraian langkah-langkahnya.

Rumus luas permukaan bola adalah 4πr², dimana ‘r’ adalah jari-jari bola. Untuk mencari jari-jari (r), kita perlu memanipulasi rumus ini. Dengan mengisolasi ‘r’, kita akan mendapatkan rumus baru untuk menghitung jari-jari bola jika luas permukaannya diketahui.

Menentukan Jari-jari dari Luas Permukaan

Untuk menentukan jari-jari bola jika luas permukaannya diketahui, kita dapat menggunakan rumus yang diturunkan dari rumus luas permukaan bola (4πr²). Dengan sedikit manipulasi aljabar, kita mendapatkan rumus: r = √(L/(4π)), di mana ‘L’ adalah luas permukaan bola. Rumus ini memungkinkan kita untuk menghitung jari-jari bola secara langsung jika nilai luas permukaannya sudah diketahui.

Contoh Soal dan Penyelesaian

Misalkan luas permukaan sebuah bola adalah 100π cm². Untuk mencari jari-jari bola tersebut, kita substitusikan nilai luas permukaan (L = 100π cm²) ke dalam rumus: r = √(L/(4π)). Maka, r = √(100π cm² / (4π)) = √(25 cm²) = 5 cm. Jadi, jari-jari bola tersebut adalah 5 cm.

Contoh Soal Cerita

Sebuah balon udara berbentuk bola memiliki luas permukaan 36π meter persegi. Berapakah jari-jari balon udara tersebut? Dengan menggunakan rumus r = √(L/(4π)), kita substitusikan L = 36π meter persegi. Maka, r = √(36π m² / (4π)) = √(9 m²) = 3 meter. Jari-jari balon udara tersebut adalah 3 meter.

Hubungan Jari-jari dan Luas Permukaan Bola

Tabel berikut menunjukkan hubungan antara jari-jari dan luas permukaan bola untuk beberapa nilai jari-jari. Perhatikan bahwa luas permukaan meningkat secara kuadratik seiring dengan bertambahnya jari-jari.

Jari-jari (r)	Luas Permukaan (4πr²)
1 cm	4π cm²
2 cm	16π cm²
3 cm	36π cm²
4 cm	64π cm²

Menentukan Jari-jari dari Luas Permukaan dalam Bentuk Persamaan

Jika luas permukaan bola dinyatakan dalam bentuk persamaan, misalnya L = 144πx², maka kita dapat menentukan jari-jari bola dengan mensubstitusikan persamaan luas permukaan ke dalam rumus jari-jari. Dalam kasus ini, kita memiliki L = 144πx². Substitusikan ke rumus r = √(L/(4π)), maka r = √(144πx²/(4π)) = √(36x²) = 6x. Jadi, jari-jari bola dalam hal x adalah 6x.

Penggunaan Satuan dan Konversi Satuan

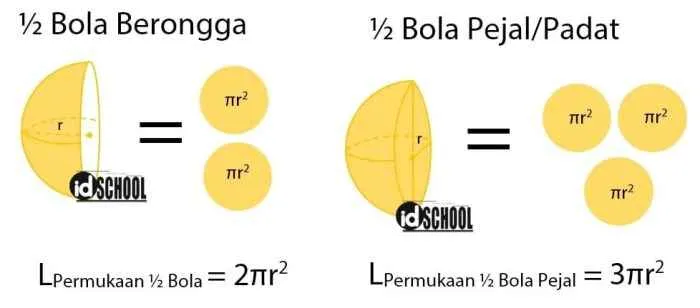
Ketepatan dalam menghitung luas permukaan bola sangat bergantung pada penggunaan satuan yang konsisten. Kesalahan kecil dalam satuan dapat berdampak signifikan pada hasil akhir, terutama dalam aplikasi praktis seperti perencanaan konstruksi atau perhitungan volume material. Oleh karena itu, memahami dan menerapkan konversi satuan merupakan keterampilan krusial dalam menyelesaikan masalah geometri.

Pentingnya Konsistensi Satuan

Konsistensi satuan merupakan kunci keberhasilan dalam perhitungan luas permukaan bola. Menggunakan satuan yang berbeda dalam satu perhitungan akan menghasilkan hasil yang salah dan menyesatkan. Misalnya, jika jari-jari bola dinyatakan dalam sentimeter (cm) dan kita menggunakan rumus dengan satuan meter (m) tanpa konversi, hasilnya akan jauh melenceng dari nilai sebenarnya.

Contoh Konversi Satuan: cm ke m dan sebaliknya

Mari kita ilustrasikan konversi satuan dengan contoh. Misalkan jari-jari bola adalah 10 cm. Untuk menghitung luas permukaannya, kita perlu mengkonversi cm ke m terlebih dahulu. Karena 1 m = 100 cm, maka 10 cm = 10/100 m = 0.1 m. Sebaliknya, jika jari-jari diberikan dalam meter, misalnya 0.5 m, maka untuk konversi ke cm, kita kalikan dengan 100, sehingga 0.5 m = 0.5 x 100 cm = 50 cm.

Contoh Soal Konversi Satuan

Sebuah bola memiliki jari-jari 15 cm. Hitung luas permukaan bola tersebut dalam meter persegi (m²). Rumus luas permukaan bola adalah 4πr², dengan r adalah jari-jari bola.

1. Konversi jari-jari dari cm ke m: 15 cm = 15/100 m = 0.15 m
2. Hitung luas permukaan: Luas = 4π(0.15 m)² = 4π(0.0225 m²) ≈ 0.2827 m²

Jadi, luas permukaan bola tersebut sekitar 0.2827 meter persegi.

Pentingnya Konsistensi Satuan dalam Perhitungan

Menggunakan satuan yang konsisten dalam perhitungan geometri, khususnya dalam menghitung luas permukaan bola, sangat penting untuk mendapatkan hasil yang akurat dan dapat diandalkan. Kegagalan dalam hal ini dapat menyebabkan kesalahan yang signifikan dan berdampak pada aplikasi praktisnya.

Langkah-langkah Sistematis Konversi Satuan

1. Identifikasi satuan yang digunakan dalam soal.
2. Tentukan satuan target yang diinginkan.
3. Cari faktor konversi yang menghubungkan kedua satuan tersebut (misalnya, 1 m = 100 cm).
4. Kalikan atau bagi nilai awal dengan faktor konversi untuk mendapatkan nilai dalam satuan target.
5. Pastikan semua perhitungan selanjutnya menggunakan satuan yang konsisten.

Kendala dan Pertimbangan dalam Perhitungan Luas Permukaan Bola

Menghitung luas permukaan bola, meskipun tampak sederhana dengan rumus 4πr², memiliki potensi jebakan yang dapat menghasilkan angka yang tidak akurat. Kesalahan kecil dalam pengukuran jari-jari atau pemahaman rumus dapat berdampak signifikan pada hasil akhir. Oleh karena itu, pemahaman yang komprehensif tentang potensi kendala dan pertimbangan penting untuk memastikan akurasi perhitungan.

Kesalahan Umum dalam Perhitungan Luas Permukaan Bola

Kesalahan umum sering muncul dari ketidaktelitian dalam pengukuran jari-jari bola. Penggunaan alat ukur yang tidak tepat atau teknik pengukuran yang salah dapat menghasilkan nilai jari-jari yang melenceng dari nilai sebenarnya. Selain itu, kesalahan dalam penggunaan rumus, seperti penggunaan nilai π yang tidak tepat (misalnya, menggunakan 3,14 sebagai pengganti nilai yang lebih presisi), juga dapat menyebabkan hasil yang tidak akurat. Terakhir, kesalahan perhitungan aritmatika sederhana, seperti kesalahan dalam perkalian atau pemangkatan, juga dapat terjadi.

Faktor yang Mempengaruhi Akurasi Perhitungan

Beberapa faktor eksternal dapat mempengaruhi akurasi perhitungan luas permukaan bola. Kondisi lingkungan, seperti suhu dan kelembaban, dapat menyebabkan perubahan dimensi bola yang kecil namun signifikan, terutama untuk bola yang terbuat dari material yang sensitif terhadap perubahan suhu. Ketidaksempurnaan bentuk bola itu sendiri, seperti penyimpangan dari bentuk bola sempurna, juga dapat mempengaruhi hasil perhitungan. Penggunaan alat ukur yang kurang presisi atau tidak terkalibrasi dengan baik juga akan mengurangi akurasi hasil.

Saran untuk Meminimalisir Kesalahan Perhitungan

Untuk meminimalisir kesalahan, penting untuk menggunakan alat ukur yang tepat dan terkalibrasi. Penggunaan jangka sorong atau mikrometer akan memberikan hasil pengukuran jari-jari yang lebih akurat dibandingkan dengan penggaris biasa. Penggunaan nilai π yang presisi, misalnya hingga beberapa digit di belakang koma, juga direkomendasikan. Lakukan pengukuran jari-jari bola beberapa kali dari berbagai sudut dan ambil nilai rata-rata untuk mengurangi kesalahan pengukuran. Terakhir, periksa kembali perhitungan dengan teliti untuk menghindari kesalahan aritmatika.

Tips dan trik: Pastikan selalu menggunakan nilai π yang akurat (minimal 3,14159), ukur jari-jari bola minimal tiga kali dari titik yang berbeda, dan gunakan kalkulator yang tepat untuk menghindari kesalahan hitung. Lakukan pengecekan silang hasil perhitungan dengan rumus alternatif atau metode lain jika memungkinkan.

Langkah-Langkah Pemeriksaan Kembali Hasil Perhitungan

Setelah perhitungan selesai, penting untuk melakukan pengecekan ulang. Pertama, periksa kembali nilai jari-jari yang digunakan, pastikan nilai tersebut akurat dan konsisten dengan pengukuran yang dilakukan. Kedua, periksa kembali langkah-langkah perhitungan, pastikan tidak ada kesalahan aritmatika seperti kesalahan dalam perkalian, pembagian, atau pemangkatan. Ketiga, bandingkan hasil perhitungan dengan estimasi kasar. Jika selisihnya signifikan, periksa kembali seluruh proses perhitungan. Keempat, jika memungkinkan, gunakan metode atau rumus alternatif untuk memverifikasi hasil.

Ringkasan Akhir

Menghitung luas kulit bola, meskipun tampak sederhana, memiliki aplikasi yang luas dan mendalam. Menguasai rumus dan teknik perhitungannya tidak hanya penting untuk menyelesaikan soal-soal matematika, tetapi juga untuk memecahkan masalah praktis di berbagai bidang. Dengan pemahaman yang kuat tentang konsep dasar dan langkah-langkah perhitungan, Anda dapat menangani tantangan perhitungan luas permukaan bola dengan mudah dan tepat. Jadi, lanjutkan eksplorasi Anda dalam dunia geometri dan aplikasikan pengetahuan ini untuk memecahkan masalah-masalah menarik lainnya.