Cara Mencari Luas Permukaan Bola Jika Diketahui Diameternya

Mengukur luas permukaan bola mungkin terdengar rumit, tetapi sebenarnya konsep ini sangat relevan dalam berbagai bidang, mulai dari mendesain stadion olahraga hingga menghitung volume tangki penyimpanan. Memahami cara menghitung luas permukaan bola, khususnya jika hanya diketahui diameternya, membuka pintu untuk memecahkan beragam permasalahan praktis. Artikel ini akan memandu Anda melalui langkah-langkah mudah dan contoh-contoh nyata untuk menguasai perhitungan ini.

Dari menghitung luas lapangan bola basket hingga mendesain kubah bangunan, kemampuan menghitung luas permukaan bola menjadi kunci. Dengan memahami rumus dan langkah-langkah perhitungan, Anda akan mampu menangani berbagai soal, baik yang sederhana maupun yang lebih kompleks. Mari kita jelajahi dunia geometri bola dan kuasai perhitungan luas permukaannya.

Rumus Luas Permukaan Bola

Menghitung luas permukaan bola merupakan keterampilan dasar dalam geometri yang memiliki aplikasi luas, mulai dari perencanaan proyek konstruksi hingga perhitungan volume dalam berbagai bidang industri. Memahami rumus ini penting untuk menyelesaikan berbagai permasalahan yang melibatkan bentuk bola, baik dalam skala kecil maupun besar.

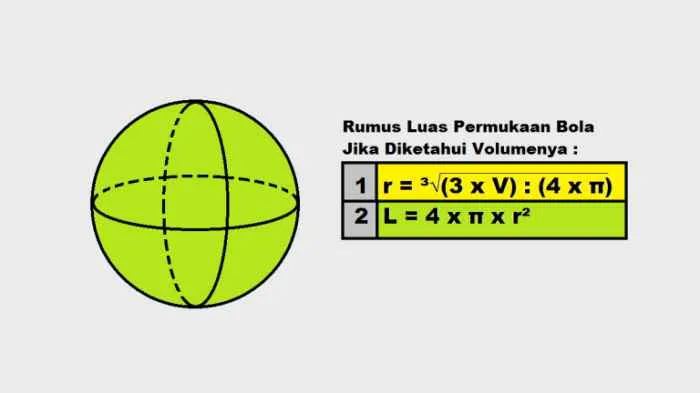
Rumus luas permukaan bola didasarkan pada jari-jari bola tersebut. Rumus ini merupakan kunci untuk menghitung area permukaan objek berbentuk bola, dan pemahamannya menjadi fondasi untuk perhitungan yang lebih kompleks.

Rumus Luas Permukaan Bola dan Variabelnya

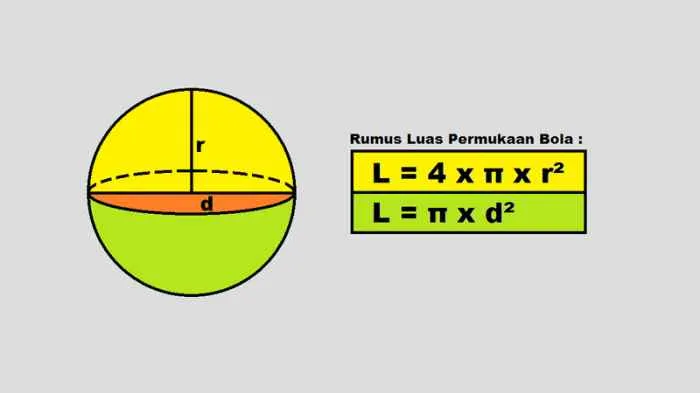
Luas permukaan bola dapat dihitung menggunakan rumus berikut:

L = 4πr²

Cara Dribbling Bola Basket Panduan Lengkap

di mana:

• L = Luas permukaan bola
• r = Jari-jari bola (setengah dari diameter)
• π (pi) ≈ 3.14159

Rumus ini menunjukkan bahwa luas permukaan bola berbanding lurus dengan kuadrat jari-jarinya. Artinya, jika jari-jari bola dilipatgandakan, maka luas permukaannya akan meningkat empat kali lipat.

Contoh Penerapan Rumus Luas Permukaan Bola

Berikut beberapa contoh penerapan rumus luas permukaan bola dengan diameter yang berbeda:

Diameter (cm)	Jari-jari (cm)	Perhitungan Luas Permukaan	Luas Permukaan (cm²)
10	5	4 * 3.14159 * 52	314.159
20	10	4 * 3.14159 * 102	1256.636
30	15	4 * 3.14159 * 152	2827.433

Ilustrasi Perhitungan Luas Permukaan Bola dengan Diameter 10 cm

Mari kita ilustrasikan perhitungan luas permukaan bola dengan diameter 10 cm. Langkah-langkahnya adalah sebagai berikut:

1. Tentukan jari-jari: Diameter adalah 10 cm, sehingga jari-jari (r) adalah 10 cm / 2 = 5 cm.
2. Substitusikan nilai ke dalam rumus: L = 4πr² = 4 * 3.14159 * 5²
3. Hitung: L = 4 * 3.14159 * 25 = 314.159 cm²

Jadi, luas permukaan bola dengan diameter 10 cm adalah sekitar 314.16 cm².

Pentingnya Memahami Rumus Luas Permukaan Bola

Memahami rumus luas permukaan bola sangat krusial dalam berbagai aplikasi praktis, mulai dari perhitungan kebutuhan cat untuk mengecat bola dunia raksasa di sebuah taman hiburan, hingga perhitungan efisiensi pendinginan pada reaktor nuklir. Ketepatan perhitungan ini berdampak langsung pada efisiensi biaya dan keamanan.

Sebutkan macam-macam cara melempar bola dalam permainan rounders

Mencari Jari-jari Bola dari Diameter

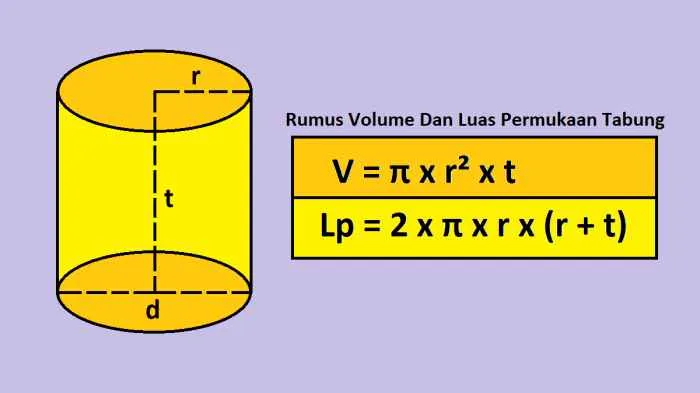
Menghitung luas permukaan bola membutuhkan pengetahuan tentang jari-jari. Namun, seringkali yang diketahui adalah diameternya. Oleh karena itu, memahami hubungan antara diameter dan jari-jari merupakan langkah krusial sebelum menghitung luas permukaan bola. Berikut penjelasan detailnya.

Hubungan Diameter dan Jari-jari Bola

Diameter bola adalah jarak terpanjang yang menghubungkan dua titik pada permukaan bola melalui pusat bola. Jari-jari bola, di sisi lain, adalah setengah dari diameternya. Dengan kata lain, jari-jari adalah jarak dari pusat bola ke titik manapun pada permukaannya. Rumusnya sederhana: Jari-jari (r) = Diameter (d) / 2.

Contoh Perhitungan Jari-jari Bola

Berikut beberapa contoh perhitungan mencari jari-jari bola jika diketahui diameternya:

1. Diameter = 10 cm, maka jari-jari = 10 cm / 2 = 5 cm
2. Diameter = 24 m, maka jari-jari = 24 m / 2 = 12 m
3. Diameter = 18 km, maka jari-jari = 18 km / 2 = 9 km

Poin-poin Penting Menentukan Jari-jari Bola

Berikut beberapa poin penting yang perlu diperhatikan saat menentukan jari-jari bola dari diameternya:

• Pastikan satuan diameter konsisten. Jika diameter dalam sentimeter, maka jari-jari juga akan dalam sentimeter.
• Pembagian diameter dengan 2 harus dilakukan dengan tepat untuk mendapatkan nilai jari-jari yang akurat.
• Perhatikan angka penting dalam perhitungan. Akurasi hasil perhitungan jari-jari bergantung pada akurasi pengukuran diameter.

Contoh Soal Cerita: Mencari Luas Permukaan Bola

Sebuah bola basket memiliki diameter 24 cm. Berapa luas permukaan bola basket tersebut? Untuk menjawab pertanyaan ini, kita perlu terlebih dahulu mencari jari-jari bola.

Jari-jari (r) = Diameter (d) / 2 = 24 cm / 2 = 12 cm

Selanjutnya, kita dapat menghitung luas permukaan bola menggunakan rumus 4πr². Dengan jari-jari 12 cm, luas permukaan bola basket adalah 4π(12 cm)² ≈ 1809.56 cm²

Kesalahan dalam menentukan jari-jari bola akan berdampak signifikan pada hasil perhitungan luas permukaan. Sebuah kesalahan kecil dalam pengukuran diameter dapat mengakibatkan kesalahan yang lebih besar pada perhitungan luas permukaan, karena jari-jari dipangkatkan dua dalam rumus luas permukaan (4πr²). Oleh karena itu, ketelitian dalam pengukuran diameter sangat penting.

Penerapan Rumus Luas Permukaan Bola

Menghitung luas permukaan bola bukan sekadar latihan matematika; aplikasinya meluas ke berbagai sektor, dari ranah olahraga hingga proyek konstruksi berskala besar. Memahami bagaimana rumus ini bekerja dan penerapannya dalam konteks nyata sangat krusial untuk memecahkan masalah praktis dan pengambilan keputusan yang tepat.

Penerapan dalam Bidang Olahraga

Dalam dunia olahraga, perhitungan luas permukaan bola memiliki implikasi signifikan, terutama dalam desain dan performa peralatan. Misalnya, pada bola basket, luas permukaan bola mempengaruhi daya cengkeram, aerodinamika, dan bahkan perilaku pantulan bola tersebut. Semakin besar luas permukaan, potensi interaksi dengan tangan pemain dan udara semakin besar, berdampak pada kontrol dan akurasi lemparan. Produsen bola basket mempertimbangkan faktor ini dalam desain bola agar memenuhi standar permainan dan preferensi pemain.

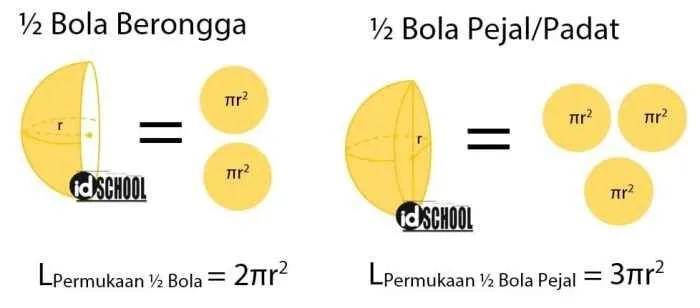
Penerapan dalam Bidang Konstruksi

Di bidang konstruksi, perhitungan luas permukaan bola sangat penting dalam perencanaan dan pembangunan struktur seperti kubah. Kubah, yang berbentuk setengah bola, memerlukan perhitungan akurat luas permukaan untuk menentukan jumlah material yang dibutuhkan, baik untuk lapisan luar maupun interior. Ketepatan perhitungan ini memastikan efisiensi penggunaan material dan ketahanan struktur. Selain itu, perhitungan ini juga krusial dalam menentukan biaya konstruksi dan jadwal pengerjaan proyek.

Contoh Soal Cerita Luas Permukaan Bola

Sebuah perusahaan sedang membangun sebuah tangki penyimpanan air berbentuk bola dengan diameter 10 meter. Berapa luas permukaan tangki tersebut? Jika biaya pengecatan per meter persegi adalah Rp 50.000, berapa total biaya pengecatan tangki tersebut?

Penyelesaian: Luas permukaan bola = 4πr². Dengan diameter 10 meter, jari-jari (r) adalah 5 meter. Maka, luas permukaan = 4π(5)² = 100π ≈ 314 meter persegi. Total biaya pengecatan = 314 meter persegi x Rp 50.000/meter persegi = Rp 15.700.000.

Hubungan Luas Permukaan dan Volume Bola

Luas permukaan bola dan volumenya memiliki hubungan matematis yang erat, meskipun keduanya mengukur aspek yang berbeda. Luas permukaan menunjukkan area permukaan luar bola, sementara volume menunjukkan kapasitas ruang yang ditempati bola. Meskipun tidak ada hubungan linier langsung, bola dengan luas permukaan yang lebih besar cenderung memiliki volume yang lebih besar juga. Namun, peningkatan luas permukaan tidak selalu berbanding lurus dengan peningkatan volume. Perubahan pada jari-jari akan memengaruhi kedua besaran ini secara berbeda.

Menghitung Luas Permukaan Bola dari Keliling Lingkaran Besar

Keliling lingkaran besar bola (K) dirumuskan sebagai K = 2πr, di mana r adalah jari-jari bola. Dari rumus ini, kita bisa mendapatkan nilai r = K/(2π). Substitusikan nilai r ini ke dalam rumus luas permukaan bola (4πr²), maka didapatkan rumus luas permukaan bola berdasarkan keliling lingkaran besarnya: Luas Permukaan = K²/(π).

Kesalahan Umum dan Cara Mengatasinya

Menghitung luas permukaan bola, meskipun terlihat sederhana, seringkali menyimpan jebakan bagi mereka yang kurang teliti. Kesalahan kecil dalam memahami rumus atau melakukan perhitungan dapat menghasilkan hasil yang jauh dari nilai sebenarnya. Pemahaman yang komprehensif tentang rumus dan langkah-langkah perhitungan, serta antisipasi terhadap kesalahan umum, sangat krusial untuk mendapatkan hasil yang akurat.

Berikut ini beberapa kesalahan umum yang sering terjadi dan bagaimana cara mengatasinya, dilengkapi dengan contoh soal yang dirancang untuk menguji pemahaman Anda.

Kesalahan Umum dalam Perhitungan Luas Permukaan Bola

Salah satu kesalahan yang paling umum adalah penggunaan rumus yang salah atau salah interpretasi terhadap besaran yang diketahui, seperti diameter dan jari-jari. Kesalahan lain muncul dari keteledoran dalam perhitungan aritmatika, khususnya dalam hal pemangkatan dan perkalian dengan π (pi).

Penyebab Kesalahan dan Cara Mengatasinya

Kesalahan Umum	Penyebab	Cara Mengatasi
Menggunakan diameter langsung dalam rumus	Tidak mengubah diameter menjadi jari-jari sebelum memasukkannya ke dalam rumus (L = 4πr²).	Pastikan untuk membagi diameter dengan 2 untuk mendapatkan jari-jari (r = d/2) sebelum melakukan perhitungan.
Kesalahan dalam perhitungan π	Penggunaan nilai π yang tidak tepat atau pembulatan yang terlalu dini.	Gunakan nilai π yang cukup akurat (misalnya, 3.14159 atau nilai π dari kalkulator). Hindari pembulatan sampai langkah akhir perhitungan.
Kesalahan dalam perhitungan pangkat dua	Kekeliruan dalam menghitung kuadrat dari jari-jari.	Periksa kembali perhitungan kuadrat jari-jari. Gunakan kalkulator jika diperlukan untuk menghindari kesalahan hitung.
Kesalahan dalam perkalian	Kekeliruan dalam mengalikan 4π dengan kuadrat jari-jari.	Lakukan perhitungan perkalian secara bertahap dan teliti. Periksa kembali setiap langkah perhitungan.

Contoh Soal dengan Jebakan

Sebuah bola memiliki diameter 14 cm. Hitunglah luas permukaan bola tersebut. (Jebakan: siswa mungkin langsung menggunakan diameter 14 cm tanpa mengubahnya menjadi jari-jari terlebih dahulu).

Penyelesaian yang benar: Jari-jari bola (r) = diameter / 2 = 14 cm / 2 = 7 cm. Luas permukaan bola (L) = 4πr² = 4π(7 cm)² = 196π cm² ≈ 615,75 cm²

Tips dan Trik Perhitungan Luas Permukaan Bola

Pastikan selalu mengubah diameter menjadi jari-jari sebelum memasukkannya ke dalam rumus. Gunakan nilai π yang akurat dan hindari pembulatan prematur. Lakukan perhitungan secara bertahap dan teliti untuk meminimalisir kesalahan. Jika memungkinkan, gunakan kalkulator untuk memastikan akurasi perhitungan.

Kesimpulan

Menguasai perhitungan luas permukaan bola, terutama jika hanya diketahui diameternya, bukan sekadar soal akademis. Kemampuan ini memiliki aplikasi praktis yang luas dalam berbagai disiplin ilmu dan kehidupan sehari-hari. Dengan memahami rumus, langkah-langkah perhitungan, dan potensi kesalahan yang mungkin terjadi, Anda akan mampu menangani beragam permasalahan yang melibatkan bola dengan lebih percaya diri dan akurat. Jadi, lanjutkan eksplorasi Anda dalam dunia geometri dan terapkan pengetahuan ini untuk memecahkan tantangan nyata.