Cara Mencari Luas Permukaan Gabungan Tabung dan Setengah Bola

Menghitung luas permukaan bangun ruang gabungan seperti tabung dan setengah bola mungkin tampak rumit, namun dengan pemahaman yang tepat terhadap rumus dan langkah-langkah perhitungan, prosesnya menjadi lebih mudah. Artikel ini akan memandu Anda melalui perhitungan luas permukaan gabungan tersebut, mulai dari memahami rumus individual hingga menyelesaikan soal-soal dengan berbagai tingkat kesulitan, termasuk kondisi-kondisi khusus seperti tabung terpotong. Siap menguasai geometri ruang?

Luas permukaan gabungan tabung dan setengah bola merupakan konsep penting dalam geometri. Memahami cara menghitungnya sangat krusial dalam berbagai aplikasi, mulai dari perencanaan konstruksi hingga desain produk. Artikel ini akan memberikan panduan komprehensif, dilengkapi contoh soal dan penyelesaian langkah demi langkah, untuk membantu Anda menguasai perhitungan ini dengan mudah dan percaya diri.

Rumus Luas Permukaan Gabungan Tabung dan Setengah Bola

Menghitung luas permukaan gabungan tabung dan setengah bola membutuhkan pemahaman mendalam terhadap rumus masing-masing bangun ruang. Kemampuan ini krusial dalam berbagai aplikasi, mulai dari perencanaan konstruksi hingga desain kemasan produk. Berikut uraian detail perhitungannya.

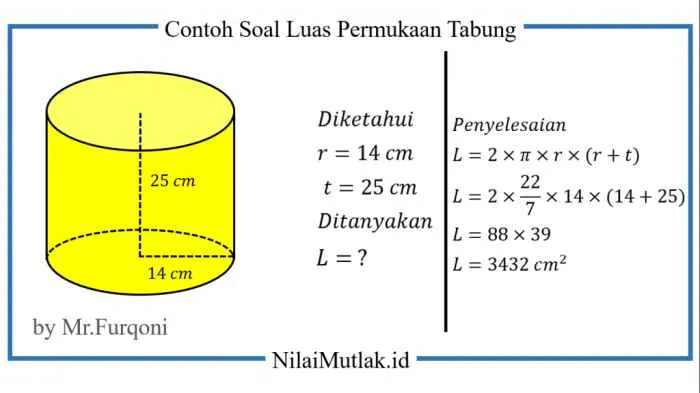
Rumus Luas Permukaan Tabung

Luas permukaan tabung terdiri dari luas selimut tabung dan luas kedua lingkaran alasnya. Rumus umum yang digunakan adalah:

L_tabung = 2πr(r + t)

di mana:

• L_tabung adalah luas permukaan tabung
• r adalah jari-jari alas tabung
• t adalah tinggi tabung

Sebagai contoh, jika sebuah tabung memiliki jari-jari 5 cm dan tinggi 10 cm, maka luas permukaannya adalah:

L_tabung = 2π(5)(5 + 10) = 150π cm² ≈ 471.24 cm²

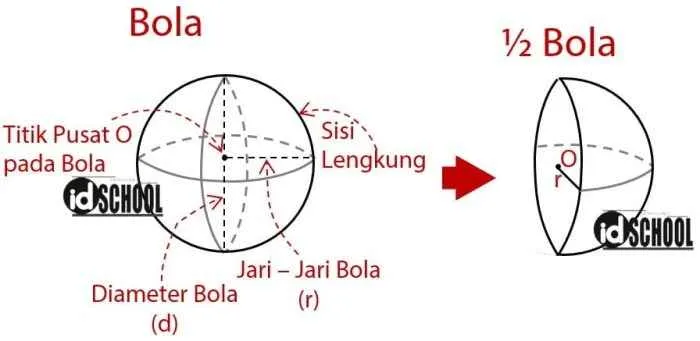
Rumus Luas Permukaan Setengah Bola

Luas permukaan setengah bola adalah setengah dari luas permukaan bola. Rumusnya adalah:

L_{setengah bola} = 2πr²

di mana:

• L_{setengah bola} adalah luas permukaan setengah bola
• r adalah jari-jari setengah bola

Misalnya, jika jari-jari setengah bola adalah 5 cm, maka luas permukaannya adalah:

L_{setengah bola} = 2π(5)² = 50π cm² ≈ 157.08 cm²

Perbandingan Rumus Luas Permukaan Tabung dan Setengah Bola

Tabel berikut merangkum perbandingan rumus luas permukaan tabung dan setengah bola:

Nama Bangun Ruang	Rumus Luas Permukaan	Penjelasan Variabel
Tabung	2πr(r + t)	r = jari-jari alas; t = tinggi tabung
Setengah Bola	2πr²	r = jari-jari setengah bola

Menghitung Luas Permukaan Gabungan Tabung dan Setengah Bola

Menghitung luas permukaan gabungan bangun ruang, khususnya tabung dan setengah bola, membutuhkan pemahaman mendalam tentang rumus luas permukaan masing-masing bangun ruang dan bagaimana menggabungkannya secara tepat. Ketelitian dalam mengidentifikasi setiap komponen permukaan yang perlu dihitung sangat krusial untuk mendapatkan hasil yang akurat. Berikut langkah-langkah sistematis untuk menghitung luas permukaan gabungan tersebut.

Langkah-langkah Perhitungan Luas Permukaan Gabungan

Perhitungan luas permukaan gabungan tabung dan setengah bola melibatkan beberapa tahapan. Mula-mula, kita perlu mengidentifikasi komponen-komponen permukaan yang akan dihitung. Selanjutnya, kita akan menerapkan rumus luas permukaan masing-masing komponen dan menjumlahkannya untuk memperoleh luas permukaan total.

1. Identifikasi Komponen Permukaan: Bangun ruang gabungan ini terdiri dari tiga komponen utama: luas permukaan selimut tabung, luas alas tabung (lingkaran), dan luas permukaan setengah bola. Perlu diperhatikan bahwa bagian lingkaran alas tabung yang terhubung dengan setengah bola tidak termasuk dalam perhitungan luas permukaan total karena tergabung dalam permukaan setengah bola.
2. Hitung Luas Permukaan Selimut Tabung: Luas permukaan selimut tabung dihitung dengan rumus 2πrt, di mana ‘r’ adalah jari-jari tabung dan ‘t’ adalah tinggi tabung.
3. Hitung Luas Alas Tabung: Luas alas tabung (lingkaran) dihitung dengan rumus πr². Namun, karena bagian ini tergabung dengan setengah bola, maka tidak dihitung.
4. Hitung Luas Permukaan Setengah Bola: Luas permukaan setengah bola dihitung dengan rumus 2πr², di mana ‘r’ adalah jari-jari setengah bola. Perhatikan bahwa jika jari-jari tabung dan setengah bola berbeda, maka gunakan jari-jari masing-masing bagian.
5. Jumlahkan Luas Permukaan: Jumlahkan luas permukaan selimut tabung dan luas permukaan setengah bola untuk mendapatkan luas permukaan gabungan total. Rumus umum: Luas Permukaan Gabungan = 2πrt + 2πr²

Contoh Perhitungan: Jari-jari Tabung dan Setengah Bola Sama

Bayangkan sebuah bangun ruang gabungan yang terdiri dari tabung dengan jari-jari r = 7 cm dan tinggi t = 10 cm, yang di atasnya terdapat setengah bola dengan jari-jari yang sama, yaitu r = 7 cm. Bangun ruang ini menyerupai sebuah silinder dengan setengah bola di bagian atasnya. Untuk memperjelas visualisasi, bayangkan sebuah kaleng minuman yang bagian atasnya membulat seperti setengah bola.

Luas permukaan selimut tabung = 2π(7 cm)(10 cm) = 140π cm²

Luas permukaan setengah bola = 2π(7 cm)² = 98π cm²

Luas permukaan gabungan = 140π cm² + 98π cm² = 238π cm² ≈ 747,7 cm²

Contoh Perhitungan: Jari-jari Tabung dan Setengah Bola Berbeda

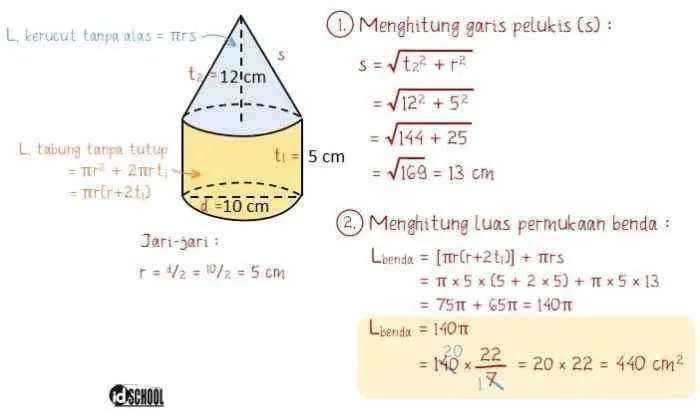
Sekarang, perhatikan kasus di mana jari-jari tabung dan setengah bola berbeda. Misalnya, tabung memiliki jari-jari r_t = 5 cm dan tinggi t = 12 cm, sedangkan setengah bola di atasnya memiliki jari-jari r_b = 6 cm. Visualisasikan ini sebagai sebuah tabung yang lebih ramping di bagian bawah, dan bagian atasnya ditutupi oleh setengah bola yang sedikit lebih besar.

Luas permukaan selimut tabung = 2π(5 cm)(12 cm) = 120π cm²

Luas permukaan setengah bola = 2π(6 cm)² = 72π cm²

Luas permukaan gabungan = 120π cm² + 72π cm² = 192π cm² ≈ 603,2 cm²

Contoh Soal dan Penyelesaian

Setelah memahami rumus perhitungan luas permukaan gabungan tabung dan setengah bola, mari kita terapkan dengan mengerjakan beberapa contoh soal. Dua contoh soal berikut akan mengilustrasikan penerapan rumus tersebut pada kasus yang berbeda, mulai dari yang sederhana hingga yang lebih kompleks. Pemahaman yang kuat terhadap konsep dasar geometri ruang sangat penting untuk menyelesaikan soal-soal ini dengan tepat.

Contoh Soal 1: Perhitungan Luas Permukaan Tabung dan Setengah Bola Sederhana

Sebuah wadah berbentuk gabungan tabung dan setengah bola memiliki tinggi tabung 10 cm dan jari-jari 7 cm. Hitung luas permukaan wadah tersebut.

Penyelesaian:

Langkah 1: Hitung luas permukaan tabung. Luas permukaan tabung = 2πr² + 2πrh, di mana r adalah jari-jari dan h adalah tinggi tabung. Dengan r = 7 cm dan h = 10 cm, maka luas permukaan tabung = 2π(7)² + 2π(7)(10) = 98π + 140π = 238π cm².

Langkah 2: Hitung luas permukaan setengah bola. Luas permukaan setengah bola = (1/2) * 4πr² = 2πr². Dengan r = 7 cm, maka luas permukaan setengah bola = 2π(7)² = 98π cm².

Langkah 3: Hitung luas permukaan total. Luas permukaan total = luas permukaan tabung + luas permukaan setengah bola = 238π + 98π = 336π cm².

Langkah 4: Hitung nilai pendekatan. Dengan menggunakan nilai π ≈ 22/7, luas permukaan total ≈ 336 * (22/7) ≈ 1056 cm².

Jadi, luas permukaan wadah tersebut sekitar 1056 cm².

Contoh Soal 2: Perhitungan Luas Permukaan Tabung dan Setengah Bola yang Lebih Kompleks

Sebuah tangki penyimpanan air berbentuk gabungan tabung dan setengah bola memiliki diameter 14 meter dan tinggi tabung 20 meter. Hitung luas permukaan tangki tersebut. Perhatikan bahwa tinggi total termasuk tinggi setengah bola.

• Menentukan jari-jari: Jari-jari (r) = diameter / 2 = 14 meter / 2 = 7 meter.
• Menentukan tinggi tabung (h_tabung): Tinggi tabung adalah tinggi total dikurangi jari-jari setengah bola. h_tabung = 20 meter – 7 meter = 13 meter.
• Menghitung luas permukaan tabung: Luas permukaan tabung = 2πr² + 2πrh_tabung = 2π(7)² + 2π(7)(13) = 98π + 182π = 280π meter².
• Menghitung luas permukaan setengah bola: Luas permukaan setengah bola = 2πr² = 2π(7)² = 98π meter².
• Menghitung luas permukaan total: Luas permukaan total = luas permukaan tabung + luas permukaan setengah bola = 280π + 98π = 378π meter².
• Nilai pendekatan: Dengan π ≈ 22/7, luas permukaan total ≈ 378 * (22/7) ≈ 1188 meter².

Dengan demikian, luas permukaan tangki penyimpanan air tersebut kira-kira 1188 meter².

Variasi Soal dan Kondisi

Menghitung luas permukaan gabungan tabung dan setengah bola merupakan aplikasi langsung dari rumus geometri. Namun, kenyataannya, soal-soal di dunia nyata seringkali melibatkan kondisi yang lebih kompleks. Pemahaman yang mendalam terhadap konsep dasar dan kemampuan untuk menyesuaikan rumus menjadi kunci untuk memecahkan masalah ini dengan akurat.

Berikut ini akan dibahas beberapa variasi soal dan kondisi yang mungkin dijumpai, termasuk bagaimana mengidentifikasi bagian permukaan yang tidak dihitung dan langkah-langkah penyelesaiannya secara detail.

Luas Permukaan Gabungan dengan Bagian Permukaan yang Tidak Dihitung

Seringkali, dalam soal luas permukaan gabungan tabung dan setengah bola, terdapat bagian permukaan yang tidak perlu dihitung karena tertutup atau tidak terlihat. Misalnya, bagian alas setengah bola yang menempel pada tabung tidak perlu dihitung jika tabung tersebut tertutup di bagian alasnya. Ketelitian dalam mengidentifikasi bagian permukaan mana yang perlu dihitung merupakan kunci untuk mendapatkan hasil yang akurat.

Sebagai contoh, bayangkan sebuah tangki penyimpanan berbentuk gabungan tabung dan setengah bola di atasnya. Jika bagian alas tabung tertutup rapat, maka luas permukaan setengah bola yang perlu dihitung hanya bagian lengkungnya saja, bukan termasuk alasnya. Rumus yang digunakan pun akan menyesuaikan dengan kondisi ini.

Contoh Soal: Tabung Terpotong

Perhatikan ilustrasi berikut: Sebuah tangki air berbentuk gabungan tabung dan setengah bola. Tabung memiliki jari-jari 7 cm dan tinggi 10 cm. Setengah bola memiliki jari-jari yang sama dengan jari-jari tabung. Namun, tabung tersebut terpotong pada bagian atasnya sehingga tinggi tabung yang tersisa adalah 8 cm. Hitunglah luas permukaan tangki air tersebut.

Ilustrasi Deskriptif: Bayangkan sebuah tangki berbentuk silinder dengan setengah bola di bagian atasnya. Bagian atas silinder terlihat terpotong, sehingga tinggi silinder yang terlihat hanya 8 cm dari tinggi total 10 cm. Jari-jari silinder dan setengah bola sama, yaitu 7 cm. Bagian alas silinder tertutup rapat, dan bagian permukaan yang perlu dihitung meliputi permukaan lengkung silinder, permukaan lengkung setengah bola, dan lingkaran di bagian atas silinder yang terpotong.

Langkah-Langkah Penyelesaian

1. Hitung luas permukaan lengkung tabung: Luas permukaan lengkung tabung = 2πrh = 2π(7 cm)(8 cm) = 112π cm²
2. Hitung luas permukaan lengkung setengah bola: Luas permukaan lengkung setengah bola = 2πr² = 2π(7 cm)² = 98π cm²
3. Hitung luas lingkaran di bagian atas tabung yang terpotong: Luas lingkaran = πr² = π(7 cm)² = 49π cm²
4. Jumlahkan semua luas permukaan: Luas permukaan total = 112π cm² + 98π cm² + 49π cm² = 259π cm² ≈ 813.7 cm²

Jadi, luas permukaan tangki air tersebut adalah sekitar 813.7 cm².

Kesalahan Umum dan Cara Mengatasinya

Kesalahan umum dalam menghitung luas permukaan gabungan seringkali disebabkan oleh kurang teliti dalam mengidentifikasi bagian permukaan yang perlu dihitung dan penggunaan rumus yang salah. Beberapa kesalahan yang sering terjadi antara lain:

• Menghitung luas alas setengah bola yang menempel pada tabung, padahal bagian tersebut tertutup.
• Menggunakan rumus luas permukaan tabung utuh, padahal tabungnya terpotong.
• Lupa menghitung luas permukaan bagian yang terlihat setelah potongan tabung.

Untuk mengatasi hal tersebut, perlu ketelitian dalam membaca soal dan menggambar sketsa bangun ruang. Pastikan untuk mengidentifikasi semua bagian permukaan yang perlu dihitung dan menggunakan rumus yang sesuai dengan kondisi yang ada. Memeriksa kembali hasil perhitungan juga penting untuk meminimalisir kesalahan.

Terakhir

Menguasai perhitungan luas permukaan gabungan tabung dan setengah bola membuka pintu menuju pemahaman yang lebih dalam tentang geometri ruang. Dengan memahami rumus dasar, langkah-langkah perhitungan, dan berbagai variasi soal, Anda kini memiliki bekal untuk menghadapi tantangan perhitungan yang lebih kompleks. Ingatlah untuk selalu teliti dalam mengidentifikasi bagian-bagian permukaan yang perlu dihitung dan cermat dalam menerapkan rumus yang tepat. Selamat mencoba!