Cara Mencari Tinggi Setengah Bola Panduan Lengkap

Menguak misteri geometri ruang seringkali membutuhkan pemahaman mendalam tentang bentuk-bentuk tiga dimensi. Salah satu bentuk yang menarik dan kerap muncul dalam berbagai aplikasi, dari arsitektur hingga teknik sipil, adalah setengah bola. Bagaimana cara kita menentukan tinggi dari bentuk setengah lingkaran tiga dimensi ini? Artikel ini akan mengupas tuntas rumus, aplikasi, dan berbagai metode untuk menghitung tinggi setengah bola, lengkap dengan contoh kasus yang relevan.

Lebih dari sekadar rumus matematika, memahami cara menghitung tinggi setengah bola membuka pintu untuk memecahkan berbagai permasalahan geometri yang lebih kompleks. Dengan pemahaman yang kuat tentang hubungan antara tinggi, volume, dan luas permukaan setengah bola, kita dapat mengaplikasikannya dalam berbagai konteks praktis. Mari kita telusuri seluk-beluk perhitungan ini dan lihat bagaimana hal tersebut dapat diterapkan dalam dunia nyata.

Rumus Mencari Tinggi Setengah Bola

Menghitung tinggi setengah bola mungkin tampak rumit, namun sebenarnya cukup sederhana jika kita memahami konsep dasarnya. Tinggi setengah bola, yang juga merupakan jari-jari bola utuhnya, berkaitan langsung dengan volume dan luas permukaannya. Pemahaman akan rumus ini penting dalam berbagai aplikasi, mulai dari perhitungan volume tangki penyimpanan hingga perencanaan konstruksi bangunan berbentuk setengah bola.

Rumus untuk menghitung tinggi setengah bola didasarkan pada jari-jari (r) bola utuh yang dibelah menjadi dua. Karena tinggi setengah bola sama dengan jari-jarinya, maka rumus yang digunakan sangatlah ringkas.

Rumus Tinggi Setengah Bola

Tinggi setengah bola (h) sama dengan jari-jari (r) bola utuh. Secara matematis, dapat ditulis sebagai:

h = r

Cara Nonton Live Streaming Bola Gratis dan Alternatifnya

Dengan demikian, jika kita mengetahui jari-jari bola, maka kita langsung mengetahui tinggi setengah bola tersebut.

Contoh Perhitungan Tinggi Setengah Bola

Mari kita lihat beberapa contoh perhitungan dengan jari-jari yang berbeda. Dengan menggunakan rumus di atas, kita akan menghitung tinggi dan volume setengah bola untuk beberapa kasus.

Jari-jari (r) (cm)	Tinggi Setengah Bola (h) (cm)	Volume Setengah Bola (V) (cm³)
5	5	≈261.8
10	10	≈2094.4
15	15	≈7068.6

Rumus volume setengah bola adalah V = (2/3)πr³. Nilai π (pi) dibulatkan menjadi 3.14159.

Langkah Perhitungan Detail (Jari-jari 5 cm)

1. Identifikasi variabel: Kita memiliki jari-jari (r) = 5 cm.
2. Hitung tinggi: Karena tinggi setengah bola sama dengan jari-jari, maka tinggi (h) = 5 cm.
3. Hitung volume: Gunakan rumus volume setengah bola: V = (2/3)πr³ = (2/3) * 3.14159 * 5³ ≈ 261.8 cm³.

Variabel dalam Rumus

Dalam rumus perhitungan tinggi dan volume setengah bola, variabel yang digunakan adalah:

• r (jari-jari): Jarak dari pusat bola ke permukaan bola. Ini merupakan input utama dalam perhitungan.
• h (tinggi): Tinggi setengah bola, yang nilainya sama dengan jari-jari (r).
• V (volume): Besarnya ruang yang ditempati oleh setengah bola. Ini merupakan output perhitungan.
• π (pi): Konstanta matematika dengan nilai ≈ 3.14159.

Hubungan Tinggi Setengah Bola dengan Volume dan Luas Permukaan

Setengah bola, sebagai bagian dari bola sempurna, memiliki hubungan matematis yang jelas antara tinggi, volume, dan luas permukaannya. Memahami hubungan ini krusial dalam berbagai aplikasi, mulai dari perhitungan kapasitas tangki penyimpanan berbentuk setengah bola hingga perencanaan proyek konstruksi yang melibatkan bentuk geometri ini. Pemahaman yang mendalam tentang rumus-rumus yang menghubungkan ketiga elemen tersebut memungkinkan perhitungan yang akurat dan efisien.

Hubungan Tinggi Setengah Bola dengan Volume

Volume setengah bola (V) dapat dihitung dengan rumus V = (2/3)πr³, di mana ‘r’ adalah jari-jari setengah bola. Karena tinggi setengah bola (h) sama dengan jari-jari (h = r), maka rumus volume dapat ditulis ulang sebagai V = (2/3)πh³. Rumus ini menunjukkan hubungan langsung dan proporsional antara volume dan kubik tinggi setengah bola. Semakin tinggi setengah bola, semakin besar volumenya, dan sebaliknya. Perlu diingat bahwa rumus ini berlaku untuk setengah bola sempurna, bukan setengah bola yang tidak beraturan.

Hubungan Tinggi Setengah Bola dengan Luas Permukaan

Luas permukaan setengah bola (A) terdiri dari luas permukaan lengkung dan luas lingkaran alasnya. Rumus luas permukaan total adalah A = 2πr² + πr², yang dapat disederhanakan menjadi A = 3πr². Karena tinggi setengah bola (h) sama dengan jari-jari (h = r), maka rumus luas permukaan dapat ditulis ulang sebagai A = 3πh². Rumus ini menunjukkan bahwa luas permukaan setengah bola berbanding lurus dengan kuadrat tingginya. Peningkatan tinggi akan mengakibatkan peningkatan luas permukaan yang lebih signifikan.

Contoh Perhitungan Tinggi Setengah Bola Berdasarkan Volume

Misalkan diketahui sebuah setengah bola memiliki volume 113,04 cm³. Kita ingin mencari tinggi setengah bola tersebut. Dengan menggunakan rumus V = (2/3)πh³, kita dapat menyelesaikannya sebagai berikut:

1. 113,04 = (2/3)πh³
2. h³ = (113,04 * 3) / (2π)
3. h³ ≈ 53.999
4. h ≈ ³√53.999 ≈ 3.77 cm

Jadi, tinggi setengah bola tersebut kurang lebih 3,77 cm.

Contoh Perhitungan Tinggi Setengah Bola Berdasarkan Luas Permukaan

Misalkan diketahui sebuah setengah bola memiliki luas permukaan 75,36 cm². Untuk mencari tinggi setengah bola, kita gunakan rumus A = 3πh²:

1. 75,36 = 3πh²
2. h² = 75,36 / (3π)
3. h² ≈ 8
4. h ≈ √8 ≈ 2.83 cm

Oleh karena itu, tinggi setengah bola tersebut kurang lebih 2,83 cm.

Ilustrasi Hubungan Tinggi, Volume, dan Luas Permukaan Setengah Bola

Bayangkan sebuah setengah bola yang terbuat dari bahan elastis. Jika kita meningkatkan tinggi setengah bola dengan cara meregangkan bahan tersebut, maka kita akan melihat peningkatan yang signifikan pada volume dan luas permukaan. Peningkatan volume akan lebih cepat daripada peningkatan tinggi karena hubungan kubiknya, sedangkan peningkatan luas permukaan akan lebih proporsional dengan kuadrat tingginya. Hubungan ini dapat divisualisasikan sebagai peningkatan ukuran keseluruhan setengah bola, dengan volume yang mengembang lebih cepat daripada luas permukaan relatif terhadap peningkatan tinggi.

Penerapan dalam Masalah Geometri

Memahami perhitungan tinggi setengah bola tak hanya berhenti pada rumus matematis. Penerapannya meluas dalam berbagai permasalahan geometri ruang, khususnya dalam mendesain dan menghitung volume bangun ruang kompleks yang melibatkan setengah bola sebagai salah satu komponennya. Kemampuan menghitung tinggi setengah bola menjadi kunci dalam menyelesaikan soal-soal geometri yang lebih menantang.

Contoh Soal Cerita Perhitungan Tinggi Setengah Bola

Sebuah kubah masjid berbentuk setengah bola dengan diameter 10 meter. Arsitek ingin memasang lampu tepat di tengah kubah, sehingga jarak lampu ke permukaan tanah harus diketahui. Berapakah tinggi lampu dari permukaan tanah jika bagian bawah kubah menyentuh tanah?

Penyelesaian:

1. Tentukan jari-jari setengah bola: Jari-jari (r) = diameter / 2 = 10 meter / 2 = 5 meter.
2. Tinggi setengah bola sama dengan jari-jarinya: Tinggi setengah bola = r = 5 meter.
3. Jadi, tinggi lampu dari permukaan tanah adalah 5 meter.

Contoh Soal Gabungan Bangun Ruang Melibatkan Setengah Bola

Sebuah wadah berbentuk gabungan tabung dan setengah bola. Tabung memiliki diameter 8 cm dan tinggi 10 cm. Setengah bola diletakkan di atas tabung dengan diameter yang sama dengan tabung. Berapakah volume total wadah tersebut?

Penyelesaian:

1. Hitung volume tabung: Volume tabung = πr²h = π(4 cm)²(10 cm) = 160π cm³
2. Hitung volume setengah bola: Volume setengah bola = (2/3)πr³ = (2/3)π(4 cm)³ = 128π/3 cm³
3. Hitung volume total: Volume total = Volume tabung + Volume setengah bola = 160π cm³ + 128π/3 cm³ ≈ 622,03 cm³

Menghitung Tinggi Setengah Bola dalam Bangun Ruang Kompleks

Bayangkan sebuah bangun ruang yang terdiri dari kerucut dan setengah bola yang dilekatkan pada alas kerucut. Tinggi kerucut adalah 12 cm dan jari-jari alasnya 5 cm. Setengah bola memiliki jari-jari yang sama dengan jari-jari alas kerucut. Untuk menghitung tinggi total bangun ruang ini, tinggi setengah bola perlu dihitung terlebih dahulu.

Penyelesaian:

1. Tinggi setengah bola sama dengan jari-jarinya, yaitu 5 cm.
2. Tinggi total bangun ruang adalah jumlah tinggi kerucut dan tinggi setengah bola: 12 cm + 5 cm = 17 cm.

Mencari Tinggi Setengah Bola dari Data yang Tidak Langsung

Menentukan tinggi setengah bola tak selalu semudah mengukur jari-jari. Terkadang, informasi yang tersedia berupa data tidak langsung, seperti volume atau luas permukaan bola utuh. Artikel ini akan membahas bagaimana kita dapat menghitung tinggi setengah bola dari data-data tersebut, dilengkapi dengan contoh soal dan penyelesaiannya.

Menentukan Tinggi Setengah Bola dari Volume Bola Utuh

Jika yang diketahui adalah volume bola utuh (V_bola), kita dapat menentukan jari-jari bola (r) terlebih dahulu. Setelah jari-jari diketahui, tinggi setengah bola (h) sama dengan jari-jari (h = r).

• Rumus volume bola: V_bola = (4/3)πr³
• Dari rumus tersebut, kita dapat mencari jari-jari (r): r = ³√[(3V_bola)/(4π)]
• Karena tinggi setengah bola sama dengan jari-jari bola, maka tinggi setengah bola (h) = r.

Menentukan Tinggi Setengah Bola dari Luas Permukaan Bola Utuh

Jika informasi yang diberikan adalah luas permukaan bola utuh (A_bola), kita dapat menentukan jari-jari bola (r) terlebih dahulu, lalu menentukan tinggi setengah bola (h).

• Rumus luas permukaan bola: A_bola = 4πr²
• Dari rumus tersebut, kita dapat mencari jari-jari (r): r = √(A_bola/(4π))
• Karena tinggi setengah bola sama dengan jari-jari bola, maka tinggi setengah bola (h) = r.

Contoh Soal dan Penyelesaian

Sebuah bola memiliki volume 36π cm³. Tentukan tinggi setengah bola tersebut.

• Diketahui: V_bola = 36π cm³
• Mencari jari-jari (r): r = ³√[(3 x 36π cm³)/(4π)] = ³√27 cm³ = 3 cm
• Tinggi setengah bola (h) = r = 3 cm

Rumus volume dan luas permukaan bola merupakan kunci untuk menentukan tinggi setengah bola secara tidak langsung. Dengan memahami hubungan antara volume/luas permukaan bola dengan jari-jari, kita dapat dengan mudah menghitung tinggi setengah bola.

Aplikasi di Dunia Nyata

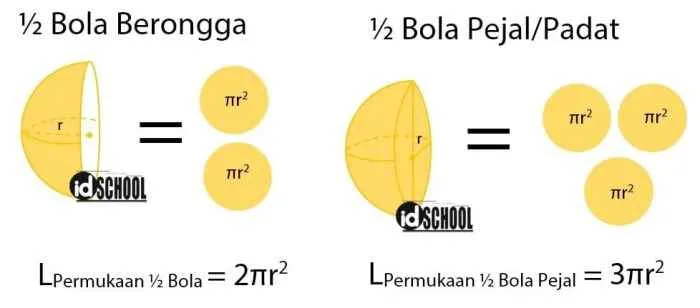
Perhitungan tinggi setengah bola, meskipun tampak sederhana, memiliki aplikasi luas di berbagai bidang. Kemampuan untuk menghitung volume dan luas permukaan setengah bola krusial dalam perencanaan dan desain berbagai proyek, dari struktur bangunan hingga infrastruktur sipil. Memahami prinsip-prinsip ini memungkinkan para profesional untuk mengoptimalkan desain, menghemat material, dan memastikan struktur yang kokoh dan efisien.

Penerapan dalam Arsitektur

Dalam arsitektur, perhitungan tinggi setengah bola sering digunakan dalam desain kubah. Kubah, dengan bentuknya yang setengah bola, memerlukan perhitungan yang akurat untuk menentukan jumlah material yang dibutuhkan dan memastikan stabilitas struktural. Misalnya, desain kubah stadion atau gedung pertunjukan sering melibatkan perhitungan yang kompleks untuk menentukan tinggi dan diameter optimal yang memenuhi kebutuhan estetika dan fungsionalitas. Perhitungan yang tepat memastikan distribusi beban yang merata dan mencegah runtuhnya struktur.

Penerapan dalam Teknik Sipil

Di bidang teknik sipil, perhitungan tinggi setengah bola berperan penting dalam perencanaan dan konstruksi berbagai infrastruktur. Contohnya, dalam desain tangki penyimpanan air bawah tanah, perhitungan volume dan luas permukaan setengah bola diperlukan untuk menentukan kapasitas penyimpanan dan kebutuhan material. Hal ini juga berlaku dalam desain terowongan atau struktur bawah tanah lainnya, di mana bentuk setengah bola dapat digunakan untuk meningkatkan kekuatan dan stabilitas struktur terhadap tekanan tanah.

Penggunaan dalam Desain Objek Tertentu

Selain kubah dan tangki penyimpanan, perhitungan tinggi setengah bola juga diterapkan dalam desain objek-objek lain. Misalnya, dalam desain lampu jalan dengan bentuk setengah bola, perhitungan akurat dibutuhkan untuk menentukan ukuran dan distribusi cahaya yang optimal. Dalam desain interior, penggunaan elemen dekoratif berbentuk setengah bola juga memerlukan perhitungan yang presisi untuk memastikan keselarasan dan estetika ruangan.

Ilustrasi Deskriptif Penerapan di Dunia Nyata

Bayangkan sebuah desain stadion sepak bola modern dengan atap berbentuk kubah setengah bola raksasa. Perhitungan tinggi setengah bola digunakan untuk menentukan tinggi kubah, memastikan ruang yang cukup untuk penonton dan lapangan, serta memastikan stabilitas struktur terhadap beban angin dan salju. Selanjutnya, perhitungan luas permukaan memungkinkan perhitungan yang akurat mengenai jumlah material yang dibutuhkan untuk konstruksi atap, yang pada akhirnya memengaruhi biaya proyek. Secara visual, kita bisa membayangkan bagaimana perhitungan yang cermat menghasilkan struktur yang kokoh dan estetis.

Bidang Studi dan Profesi yang Membutuhkan Perhitungan Tinggi Setengah Bola

• Arsitektur
• Teknik Sipil
• Teknik Mesin
• Teknik Kimia (desain tangki penyimpanan)
• Desain Interior
• Perencanaan Kota (dalam konteks desain bangunan publik)

Kesimpulan

Menentukan tinggi setengah bola, meskipun tampak sederhana, ternyata memiliki implikasi yang luas dalam berbagai bidang. Mulai dari perhitungan volume dan luas permukaan hingga penerapannya dalam desain bangunan dan infrastruktur, kemampuan untuk menghitung tinggi setengah bola merupakan keterampilan penting yang dibutuhkan dalam berbagai profesi. Dengan memahami berbagai metode perhitungan, termasuk perhitungan langsung dan tidak langsung, kita dapat mengoptimalkan solusi untuk berbagai permasalahan geometri yang kompleks dan menantang.