Cara Mencari Volume Bola Rumus, Contoh, dan Penerapannya

Bayangkan sebuah bola basket, bola dunia, atau bahkan gelembung sabun. Semua benda ini memiliki bentuk bola, dan memahami cara menghitung volumenya punya implikasi luas, mulai dari perencanaan konstruksi hingga peramalan cuaca. Memahami rumus volume bola bukanlah sekadar soal matematika; ini adalah kunci untuk mengukur dan memahami dunia tiga dimensi di sekitar kita. Artikel ini akan mengupas tuntas cara mencari volume bola, mulai dari rumus dasar hingga aplikasi praktisnya dalam berbagai konteks.

Dari perhitungan sederhana hingga permasalahan yang lebih kompleks, kita akan menjelajahi berbagai metode dan contoh soal yang akan membantu Anda menguasai konsep ini. Dengan pemahaman yang komprehensif, Anda akan mampu menyelesaikan berbagai permasalahan yang melibatkan volume bola dengan percaya diri. Siap untuk menyelami dunia geometri tiga dimensi?

Rumus Volume Bola

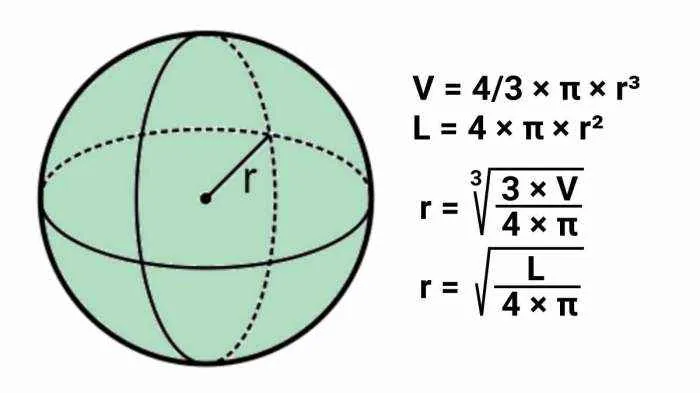
Menghitung volume bola merupakan hal fundamental dalam berbagai bidang, mulai dari ilmu fisika dan teknik hingga arsitektur dan desain. Pemahaman yang tepat tentang rumus volume bola dan penerapannya sangat krusial untuk menyelesaikan berbagai permasalahan yang melibatkan bentuk tiga dimensi ini. Artikel ini akan mengulas secara detail rumus volume bola, beserta contoh penerapan dan penurunan rumusnya secara geometri.

Rumus dan Variabel

Rumus untuk menghitung volume bola adalah:

V = (4/3)πr³

di mana:

• V = Volume bola
• r = Jari-jari bola
• π (pi) ≈ 3,14159

Rumus ini menyatakan bahwa volume bola berbanding lurus dengan pangkat tiga jari-jarinya. Semakin besar jari-jari bola, semakin besar pula volumenya, dengan faktor pengali (4/3)π.

Contoh Penerapan Rumus

Mari kita terapkan rumus tersebut dengan beberapa contoh nilai jari-jari yang berbeda.

Contoh 1: Jika jari-jari bola (r) adalah 5 cm, maka volumenya adalah:

V = (4/3)π(5 cm)³ ≈ 523,6 cm³

Contoh 2: Jika jari-jari bola (r) adalah 10 cm, maka volumenya adalah:

V = (4/3)π(10 cm)³ ≈ 4188,8 cm³

Cara Membuat Bola Daging Agar Tidak Hancur

Perhatikan bahwa dengan menggandakan jari-jari, volume bola menjadi delapan kali lipat (10³ / 5³ = 8).

Tabel Volume Bola Berdasarkan Jari-jari

Tabel berikut merangkum volume bola untuk berbagai nilai jari-jari:

Jari-jari (r) (cm)	Volume (V) (cm³)
1	4,19
2	33,51
3	113,10
4	268,08

Penurunan Rumus Volume Bola Secara Geometri

Penurunan rumus volume bola secara geometri melibatkan konsep integral kalkulus. Secara sederhana, kita dapat membayangkan bola sebagai kumpulan dari banyak sekali cakram tipis dengan jari-jari yang berbeda-beda. Volume setiap cakram dapat dihitung dengan rumus luas lingkaran (πr²) dikalikan dengan ketebalan cakram (dy). Dengan mengintegralkan luas semua cakram tersebut sepanjang sumbu y dari -r hingga r, kita akan mendapatkan rumus volume bola. Proses integrasi ini menghasilkan rumus (4/3)πr³.

Visualisasikan bola dipotong menjadi irisan-irisan tipis berbentuk lingkaran. Luas setiap lingkaran adalah πr², dengan r bergantung pada posisi irisan sepanjang sumbu y. Dengan mengintegralkan luas semua lingkaran tersebut dari -r hingga r, kita akan memperoleh volume total bola.

Langkah-langkah Perhitungan Volume Bola

Berikut langkah-langkah sistematis untuk menghitung volume bola:

1. Tentukan nilai jari-jari bola (r).
2. Pangkat tiga nilai jari-jari (r³).
3. Kalikan hasil pangkat tiga dengan (4/3)π.
4. Hasil akhir merupakan volume bola (V).

Sebagai contoh, jika r = 7 cm:

1. r = 7 cm
2. r³ = 343 cm³
3. (4/3)π(343 cm³) ≈ 1436,8 cm³
4. V ≈ 1436,8 cm³

Mencari Jari-jari Bola

Menentukan volume bola merupakan langkah awal untuk memahami karakteristik geometriknya. Namun, seringkali kita justru membutuhkan informasi sebaliknya: jari-jari bola jika volumenya sudah diketahui. Kemampuan untuk menghitung jari-jari ini krusial dalam berbagai aplikasi, mulai dari perencanaan konstruksi hingga analisis data ilmiah. Berikut ini langkah-langkah dan contoh penerapannya.

Mencari Jari-jari Bola jika Diketahui Volumenya

Rumus volume bola adalah ⁴⁄₃πr³, dengan r adalah jari-jari bola. Untuk mencari jari-jari (r), rumus tersebut dapat dibalik. Prosesnya melibatkan manipulasi aljabar untuk mengisolasi variabel r. Pertama, kalikan kedua sisi persamaan dengan ³⁄₄ untuk menghilangkan koefisien ⁴⁄₃. Kemudian, bagi kedua sisi dengan π. Terakhir, ambil akar pangkat tiga dari kedua sisi untuk mendapatkan nilai r.

Sebagai contoh, jika volume bola adalah 36π cm³, maka:

36π = ⁴⁄₃πr³

r³ = (³⁄₄) * 36

r³ = 27

r = ³√27 = 3 cm

Jadi, jari-jari bola tersebut adalah 3 cm.

Contoh Soal Cerita Pencarian Jari-jari Bola

Sebuah balon udara berbentuk bola memiliki volume 113,04 cm³. Berapa jari-jari balon udara tersebut, asumsikan π = 3,14?

Penyelesaian:

V = ⁴⁄₃πr³

113,04 = ⁴⁄₃ * 3,14 * r³

r³ = (113,04 * 3) / (4 * 3,14)

r³ = 27

r = ³√27 = 3 cm

Jari-jari balon udara tersebut adalah 3 cm.

Mencari Jari-jari Bola jika Diketahui Luas Permukaannya

Luas permukaan bola dirumuskan sebagai 4πr². Jika luas permukaan diketahui, kita dapat mencari jari-jari dengan membagi luas permukaan dengan 4π, lalu mengambil akar kuadrat hasilnya. Setelah mendapatkan jari-jari, volume bola dapat dihitung menggunakan rumus volume bola yang telah dijelaskan sebelumnya. Dengan demikian, mengetahui luas permukaan secara tidak langsung memungkinkan kita untuk menghitung volumenya dan sebaliknya.

Misalnya, jika luas permukaan bola adalah 100π cm²:

100π = 4πr²

r² = 25

r = 5 cm

Dengan jari-jari 5 cm, volume bola dapat dihitung sebagai ⁴⁄₃π(5³) = ⁵⁰⁰⁄₃π cm³.

Mencari Jari-jari Bola jika Diketahui Volume dan Informasi Tambahan

Jika hanya diketahui volume setengah bola, kita perlu menyesuaikan rumus volume. Volume setengah bola adalah setengah dari volume bola penuh, yaitu ²⁄₃πr³. Dengan informasi volume setengah bola, kita dapat mencari jari-jari dengan cara yang serupa seperti mencari jari-jari bola penuh, hanya saja kita menggunakan rumus volume setengah bola.

Contoh: Volume setengah bola adalah 27π cm³. Maka:

27π = ²⁄₃πr³

r³ = (27 * 3) / 2

r³ = 40.5

r = ³√40.5 ≈ 3.43 cm

Dengan demikian, jari-jari setengah bola tersebut kira-kira 3.43 cm.

Penerapan Rumus Volume Bola dalam Masalah

Memahami rumus volume bola, yaitu V = 4/3 πr³, bukan hanya sekadar menghafal formula matematis. Penerapannya sangat luas, mulai dari perhitungan sederhana hingga permasalahan yang lebih kompleks dalam berbagai bidang. Pemahaman yang mendalam tentang rumus ini memungkinkan kita untuk menyelesaikan berbagai masalah yang melibatkan objek berbentuk bola atau mendekati bentuk bola.

Kemampuan menyelesaikan soal cerita yang berkaitan dengan volume bola menuntut pemahaman konseptual yang kuat dan kemampuan mengaplikasikan rumus dengan tepat. Berikut ini beberapa contoh soal cerita dan langkah penyelesaiannya untuk mengilustrasikan penerapan rumus volume bola.

Contoh Soal Cerita dan Penyelesaiannya

Berikut tiga contoh soal cerita yang berbeda yang memerlukan perhitungan volume bola untuk menyelesaikannya, beserta langkah-langkah penyelesaian dan tabel perbandingannya.

1. Sebuah bola kasti memiliki diameter 10 cm. Berapa volume bola kasti tersebut?
2. Sebuah balon udara berbentuk bola memiliki jari-jari 5 meter saat terisi penuh. Berapa volume udara di dalam balon tersebut?
3. Sebuah tangki penyimpanan air berbentuk setengah bola dengan jari-jari 2 meter. Berapa volume air maksimum yang dapat ditampung tangki tersebut?

Langkah-langkah penyelesaian untuk masing-masing soal tersebut adalah sebagai berikut:

1. Soal 1: Diketahui diameter = 10 cm, maka jari-jari (r) = 5 cm. Substitusikan nilai r ke dalam rumus: V = 4/3 π(5)³ ≈ 523,6 cm³. Jadi, volume bola kasti tersebut sekitar 523,6 cm³.
2. Soal 2: Diketahui jari-jari (r) = 5 meter. Substitusikan nilai r ke dalam rumus: V = 4/3 π(5)³ ≈ 523,6 m³. Jadi, volume udara di dalam balon tersebut sekitar 523,6 m³.
3. Soal 3: Diketahui jari-jari (r) = 2 meter. Karena tangki berbentuk setengah bola, maka volume air maksimum adalah setengah dari volume bola penuh. V = (1/2) * (4/3) π(2)³ ≈ 16,76 m³. Jadi, volume air maksimum yang dapat ditampung tangki tersebut sekitar 16,76 m³.

Tabel Perbandingan Contoh Soal

No.	Deskripsi Soal	Rumus yang Digunakan	Langkah Penyelesaian Singkat
1	Volume bola kasti dengan diameter 10 cm	V = 4/3 πr³	r = 5 cm; V ≈ 523,6 cm³
2	Volume balon udara berbentuk bola dengan jari-jari 5 meter	V = 4/3 πr³	r = 5 m; V ≈ 523,6 m³
3	Volume tangki air berbentuk setengah bola dengan jari-jari 2 meter	V = (1/2) * (4/3) πr³	r = 2 m; V ≈ 16,76 m³

Penerapan Rumus Volume Bola dalam Dunia Nyata

Rumus volume bola memiliki aplikasi yang luas di dunia nyata. Sebagai contoh, dalam industri manufaktur, perhitungan volume bola digunakan untuk menentukan jumlah material yang dibutuhkan dalam pembuatan bola-bola berongga untuk berbagai keperluan, seperti bola lampu atau bantalan. Dalam bidang meteorologi, perhitungan volume awan (yang diasumsikan berbentuk bola) dapat membantu dalam prediksi cuaca. Lebih jauh lagi, perhitungan volume bola juga digunakan dalam perencanaan infrastruktur, seperti perhitungan volume material yang dibutuhkan untuk membangun kubah atau tangki penyimpanan berbentuk bola.

Sebagai ilustrasi, perhitungan volume bola dunia (dengan mengasumsikan bentuknya sebagai bola sempurna) membutuhkan data mengenai jari-jari bumi. Dengan data jari-jari bumi yang akurat, kita dapat menghitung volume bumi dengan menggunakan rumus yang sama. Begitu pula dengan perhitungan volume bola lampu, dengan mengetahui jari-jari bola lampu, kita dapat menghitung volume ruang di dalam bola lampu tersebut.

Konsep Terkait Volume Bola

Memahami volume bola merupakan langkah awal untuk menguasai berbagai konsep geometri ruang. Namun, pemahaman tersebut akan lebih komprehensif jika dikaitkan dengan konsep-konsep terkait lainnya, seperti luas permukaan, perbandingan dengan bangun ruang lain, kepadatan, dan pengaruh perubahan jari-jari terhadap volume.

Luas Permukaan Bola dan Hubungannya dengan Volume

Luas permukaan bola dan volumenya saling berkaitan erat. Luas permukaan bola dihitung dengan rumus 4πr², di mana r adalah jari-jari bola. Sementara volume bola dihitung dengan rumus (4/3)πr³. Perhatikan bahwa kedua rumus tersebut melibatkan jari-jari bola sebagai variabel utama. Hubungannya terletak pada fakta bahwa perubahan jari-jari akan memengaruhi baik luas permukaan maupun volume bola secara proporsional, meskipun dengan pangkat yang berbeda. Peningkatan jari-jari akan meningkatkan baik luas permukaan maupun volume, namun peningkatan volume akan lebih signifikan karena pangkat tiga pada rumusnya.

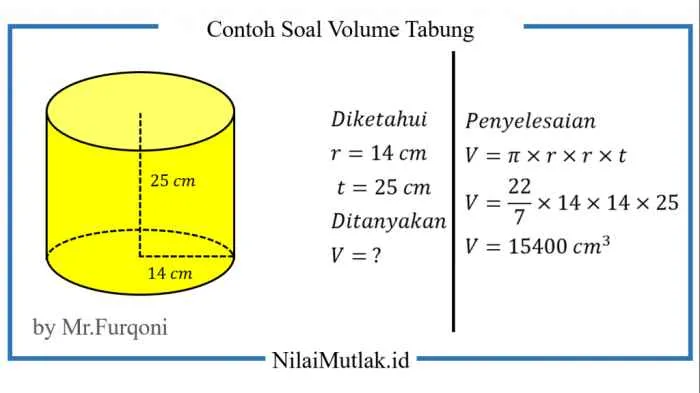
Perbandingan Volume Bola, Kerucut, dan Tabung

Bola, kerucut, dan tabung merupakan bangun ruang yang berbeda dengan rumus volume yang unik. Volume bola, seperti yang telah dijelaskan, adalah (4/3)πr³. Volume kerucut adalah (1/3)πr²t, di mana r adalah jari-jari alas dan t adalah tinggi kerucut. Sementara volume tabung adalah πr²t, dengan r sebagai jari-jari alas dan t sebagai tinggi tabung. Perbandingan ketiganya bergantung pada nilai jari-jari dan tinggi masing-masing bangun ruang. Tidak ada perbandingan universal karena hasilnya sangat kontekstual dan bergantung pada dimensi masing-masing bangun ruang.

Perbedaan Volume dan Luas Permukaan Bola

Volume bola mengukur ruang tiga dimensi yang ditempati oleh bola, sedangkan luas permukaan bola mengukur luas total permukaan bola dua dimensi. Meskipun keduanya terkait dengan jari-jari bola, keduanya mengukur aspek yang berbeda dari bangun ruang tersebut. Volume menunjukkan kapasitas bola, sedangkan luas permukaan menunjukkan ukuran total permukaannya.

Kepadatan dan Hubungannya dengan Volume Bola

Kepadatan suatu benda didefinisikan sebagai massa per satuan volume (ρ = m/V). Jika massa (m) suatu bola diketahui, dan volume (V) bola telah dihitung menggunakan rumus (4/3)πr³, maka kepadatan bola dapat ditentukan. Misalnya, jika sebuah bola memiliki massa 100 gram dan jari-jari 5 cm, maka volumenya adalah (4/3)π(5³) ≈ 523,6 cm³. Kepadatannya kemudian adalah 100 gram / 523,6 cm³ ≈ 0,19 gram/cm³. Konsep ini penting dalam berbagai aplikasi, seperti menentukan jenis material bola berdasarkan kepadatannya.

Pengaruh Perubahan Jari-jari terhadap Volume Bola

Volume bola bergantung secara kubik pada jari-jari. Artinya, jika jari-jari bola digandakan, volumenya akan meningkat delapan kali lipat (2³ = 8). Sebaliknya, jika jari-jari dibagi dua, volumenya akan menjadi 1/8 dari volume semula. Hubungan ini menunjukkan bahwa perubahan kecil pada jari-jari akan menghasilkan perubahan yang signifikan pada volume bola. Sebagai contoh, sebuah bola dengan jari-jari 2 cm memiliki volume sekitar 33,5 cm³, sementara bola dengan jari-jari 4 cm memiliki volume sekitar 268 cm³, delapan kali lebih besar.

Penutup

Menguasai cara menghitung volume bola membuka pintu menuju pemahaman yang lebih dalam tentang geometri dan aplikasinya di dunia nyata. Dari perencanaan infrastruktur hingga inovasi teknologi, kemampuan untuk menghitung volume bola berperan penting. Dengan memahami rumus, langkah-langkah perhitungan, dan berbagai contoh penerapannya, Anda kini memiliki bekal yang kuat untuk menghadapi berbagai tantangan perhitungan volume bola, baik dalam konteks akademis maupun profesional. Semoga pemahaman ini menginspirasi Anda untuk terus mengeksplorasi keajaiban matematika.