Cara Menemukan Rumus Luas Permukaan Bola

Bola, bentuk geometris yang sederhana namun elegan, menyimpan misteri matematika yang menarik. Dari bola sepak hingga planet-planet di tata surya, bentuk bola hadir di berbagai skala. Memahami luas permukaan bola bukan sekadar soal rumus, tetapi kunci untuk mengungkap rahasia ukuran dan volume benda-benda bulat di sekitar kita. Perjalanan kita kali ini akan mengupas tuntas bagaimana rumus tersebut ditemukan, serta penerapannya dalam kehidupan sehari-hari.

Menguak misteri rumus luas permukaan bola membutuhkan pemahaman konsep dasar geometri, khususnya tentang jari-jari dan diameter. Kita akan menjelajahi langkah-langkah deduktif untuk menurunkan rumus, membandingkannya dengan bangun ruang lain, dan mengaplikasikannya lewat contoh soal yang relevan. Siap untuk menyelami dunia geometri bola?

Pemahaman Konsep Bola

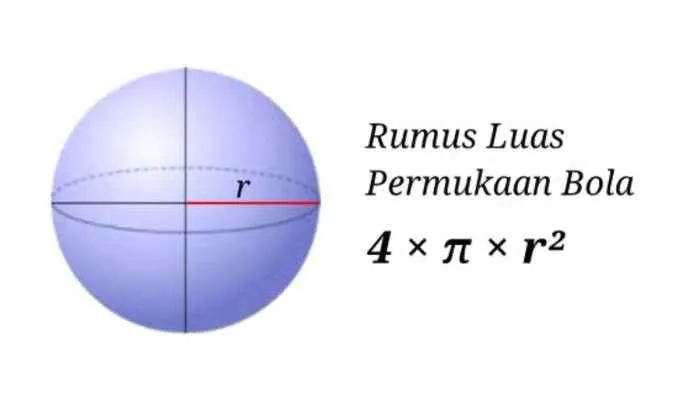
Bola, dalam geometri, merupakan bangun ruang tiga dimensi yang dibentuk oleh himpunan semua titik dalam ruang yang berjarak sama terhadap suatu titik tetap yang disebut pusat bola. Pemahaman tentang bola dan rumus luas permukaannya memiliki aplikasi luas, mulai dari perhitungan volume tangki penyimpanan hingga perencanaan konstruksi kubah stadion.

Memahami konsep bola tidak hanya sebatas definisi matematisnya, tetapi juga mencakup pemahaman tentang unsur-unsurnya dan bagaimana unsur-unsur tersebut saling berkaitan dalam menentukan sifat-sifat geometris bola. Penguasaan konsep ini menjadi kunci untuk menyelesaikan berbagai permasalahan yang melibatkan bangun ruang ini.

Unsur-unsur Penting Bola

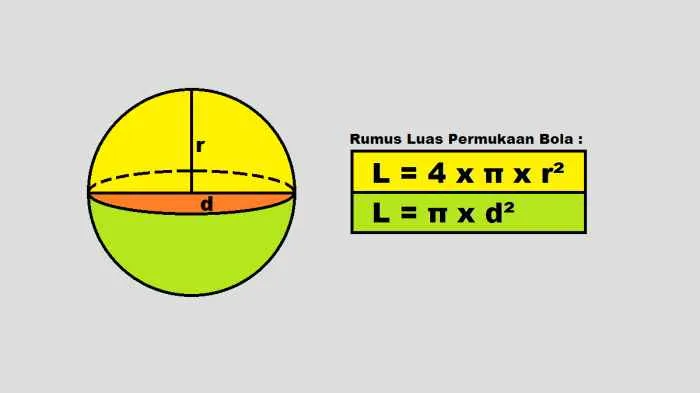
Bola memiliki beberapa unsur penting yang perlu dipahami untuk menghitung luas permukaannya. Unsur-unsur tersebut antara lain jari-jari, diameter, dan luas permukaan itu sendiri. Jari-jari (r) adalah jarak dari pusat bola ke titik manapun pada permukaan bola. Diameter (d) adalah garis lurus yang melalui pusat bola dan menghubungkan dua titik pada permukaan bola. Diameter selalu dua kali panjang jari-jari (d = 2r). Luas permukaan bola merupakan jumlah total area permukaan bola tersebut.

Ilustrasi Bola dan Pengaruh Jari-jari

Bayangkan sebuah bola sempurna. Titik tengah bola adalah pusatnya. Garis yang menghubungkan pusat bola ke titik manapun di permukaannya adalah jari-jari (r). Garis yang melewati pusat dan menghubungkan dua titik berlawanan di permukaan adalah diameter (d). Semakin besar jari-jari bola, semakin besar pula luas permukaannya. Ilustrasi ini dapat digambarkan sebagai dua bola, satu dengan jari-jari kecil dan satu lagi dengan jari-jari besar. Bola dengan jari-jari yang lebih besar akan memiliki area permukaan yang secara signifikan lebih luas dibandingkan bola dengan jari-jari yang lebih kecil. Perbedaan luas permukaan ini sebanding dengan kuadrat dari perbandingan jari-jari kedua bola tersebut.

Contoh Objek Berbentuk Bola

Bola sebagai bentuk geometris murni ditemukan dalam berbagai objek di kehidupan nyata. Beberapa contohnya termasuk bola sepak, bola basket, planet-planet (yang mendekati bentuk bola), benda langit lainnya, hingga butiran pasir yang mendekati bentuk bola. Bentuk bola ini seringkali idealisasi dari bentuk objek sebenarnya yang mungkin sedikit tidak sempurna.

Perbandingan Rumus Luas Permukaan Bola dengan Bangun Ruang Lainnya

Rumus luas permukaan bola berbeda dengan rumus luas permukaan bangun ruang lainnya. Perbedaan ini mencerminkan perbedaan bentuk dan sifat geometris masing-masing bangun ruang. Berikut perbandingan rumus luas permukaan bola dengan kubus dan tabung:

Bangun Ruang	Rumus Luas Permukaan
Bola	4πr²
Kubus (dengan sisi s)	6s²
Tabung (dengan jari-jari r dan tinggi t)	2πr² + 2πrt

Mencari Rumus Luas Permukaan Bola

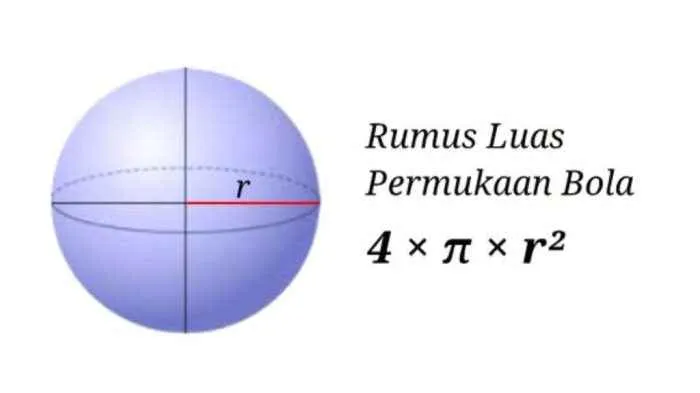
Menentukan luas permukaan bola mungkin tampak rumit, namun dengan pendekatan deduktif yang tepat, kita dapat menurunkan rumusnya dengan mudah. Pemahaman ini penting tidak hanya dalam matematika, tetapi juga dalam berbagai aplikasi praktis, dari perencanaan proyek konstruksi hingga perhitungan kebutuhan material dalam industri manufaktur. Berikut uraian langkah-langkahnya.

Penurunan Rumus Luas Permukaan Bola

Kita akan menggunakan pendekatan membayangkan bola sebagai kumpulan sejumlah besar kerucut kecil yang membentuk permukaannya. Bayangkan bola dibagi menjadi banyak sekali irisan tipis, seperti jeruk yang dipotong-potong. Setiap irisan dapat dianggap sebagai lingkaran dengan keliling tertentu. Jika kita “buka” setiap irisan ini dan merentangkannya, kita akan mendapatkan bentuk yang mendekati segitiga. Dengan menjumlahkan luas semua segitiga kecil ini, kita bisa mendekati luas permukaan bola.

Langkah pertama adalah mempertimbangkan sebuah kerucut kecil yang membentuk sebagian kecil dari permukaan bola. Tinggi kerucut ini mendekati jari-jari bola (r), dan keliling alasnya merupakan sebagian kecil dari keliling bola (2πr). Luas segitiga yang terbentuk kira-kira setengah dari hasil kali tinggi kerucut dengan keliling alasnya. Dengan jumlah kerucut yang sangat banyak, penjumlahan luas semua segitiga ini akan mendekati luas permukaan bola. Melalui kalkulus, penjumlahan ini menghasilkan rumus luas permukaan bola: 4πr².

Perbandingan dengan Rumus Luas Permukaan Bangun Ruang Lainnya

Rumus luas permukaan bola berbeda secara signifikan dengan rumus bangun ruang lainnya. Perbedaan ini muncul karena bentuk bola yang unik dan tiga dimensi tanpa sudut atau sisi datar. Sebagai contoh, rumus luas permukaan kubus adalah 6s², di mana s adalah panjang sisi kubus. Rumus ini jauh lebih sederhana daripada rumus bola karena kubus memiliki sisi-sisi yang datar dan mudah dihitung luasnya. Begitu pula dengan luas permukaan balok, limas, dan tabung, semuanya memiliki rumus yang bergantung pada dimensi linear seperti panjang, lebar, dan tinggi.

Tabel Rumus Luas Permukaan Berbagai Bangun Ruang

Bangun Ruang	Rumus Luas Permukaan
Kubus	6s²
Balok	2(pl + pt + lt)
Tabung	2πr(r + t)
Bola	4πr²
Limas Segiempat	Luas alas + 4 x Luas segitiga tegak

Penerapan Rumus Luas Permukaan Bola pada Contoh Soal

Misalkan kita ingin menghitung luas permukaan bola dengan jari-jari 7 cm. Kita gunakan rumus luas permukaan bola: 4πr². Dengan mensubstitusikan r = 7 cm, kita peroleh:

4π(7 cm)² = 4π(49 cm²) ≈ 615,75 cm²

Jadi, luas permukaan bola dengan jari-jari 7 cm adalah sekitar 615,75 cm².

Penerapan Rumus Luas Permukaan Bola

Rumus luas permukaan bola, 4πr², memiliki aplikasi luas dalam berbagai bidang, mulai dari desain arsitektur hingga ilmu kedokteran. Memahami penerapan rumus ini memungkinkan kita untuk menyelesaikan berbagai permasalahan yang melibatkan objek berbentuk bola atau mendekati bola. Berikut beberapa contoh penerapannya dalam kehidupan sehari-hari.

Contoh Penerapan Rumus Luas Permukaan Bola

Berikut ini tiga contoh soal penerapan rumus luas permukaan bola dalam konteks kehidupan sehari-hari, beserta penyelesaian langkah demi langkah dan ringkasannya dalam tabel.

1. Soal 1: Sebuah balon udara berbentuk bola memiliki jari-jari 7 meter. Berapa luas permukaan balon udara tersebut?
2. Penyelesaian:
   1. Diketahui: jari-jari (r) = 7 meter
   2. Rumus: Luas permukaan bola = 4πr²
   3. Penyelesaian: Luas permukaan = 4 × π × (7 meter)² = 4 × π × 49 meter² ≈ 615,75 meter²
3. Soal 2: Sebuah bola basket memiliki diameter 24 cm. Hitung luas permukaan bola basket tersebut.
4. Penyelesaian:
   1. Diketahui: diameter (d) = 24 cm, maka jari-jari (r) = d/2 = 12 cm
   2. Rumus: Luas permukaan bola = 4πr²
   3. Penyelesaian: Luas permukaan = 4 × π × (12 cm)² = 4 × π × 144 cm² ≈ 1809,56 cm²
5. Soal 3: Sebuah tangki penyimpanan air berbentuk setengah bola dengan jari-jari 5 meter. Berapa luas permukaan bagian luar tangki tersebut (termasuk alasnya)?
6. Penyelesaian:
   1. Diketahui: jari-jari (r) = 5 meter
   2. Luas permukaan setengah bola = ½(4πr²) + πr² = 3πr²
   3. Penyelesaian: Luas permukaan = 3 × π × (5 meter)² = 75π meter² ≈ 235,62 meter²

Ringkasan Soal dan Penyelesaian

Soal	Data Diketahui	Rumus	Jawaban
Luas permukaan balon udara	r = 7 meter	4πr²	≈ 615,75 meter²
Luas permukaan bola basket	d = 24 cm (r = 12 cm)	4πr²	≈ 1809,56 cm²
Luas permukaan tangki air (setengah bola)	r = 5 meter	3πr²	≈ 235,62 meter²

Perbedaan Pendekatan Penyelesaian Soal Jika Diketahui Diameter

Perbedaan utama terletak pada langkah awal. Jika diketahui diameter, kita perlu membagi diameter dengan dua untuk mendapatkan jari-jari (r) sebelum menerapkan rumus luas permukaan bola (4πr²). Langkah ini memastikan bahwa kita menggunakan nilai jari-jari yang benar dalam perhitungan.

Soal Cerita Menantang Luas Permukaan Bola

Sebuah perusahaan mainan merencanakan produksi bola dunia raksasa untuk taman bermain. Bola dunia tersebut direncanakan memiliki diameter 10 meter dan akan dicat dengan dua warna, biru untuk lautan dan hijau untuk daratan. Jika rasio luas permukaan lautan terhadap daratan adalah 7:3, berapa luas permukaan yang akan dicat dengan warna biru?

Variasi Soal dan Penyelesaian

Setelah memahami rumus luas permukaan bola, 4πr², penting untuk mengasah pemahaman dengan berlatih soal. Menguasai rumus saja tidak cukup; kemampuan menerapkannya dalam berbagai konteks soal merupakan kunci utama. Berikut beberapa variasi soal dan penyelesaiannya yang akan menguji kemampuan Anda.

Soal dan Penyelesaian Luas Permukaan Bola

Berikut dua contoh soal yang mengharuskan perhitungan jari-jari atau diameter bola jika luas permukaannya diketahui. Perhatikan bagaimana rumus luas permukaan bola dimanipulasi untuk menemukan variabel yang belum diketahui.

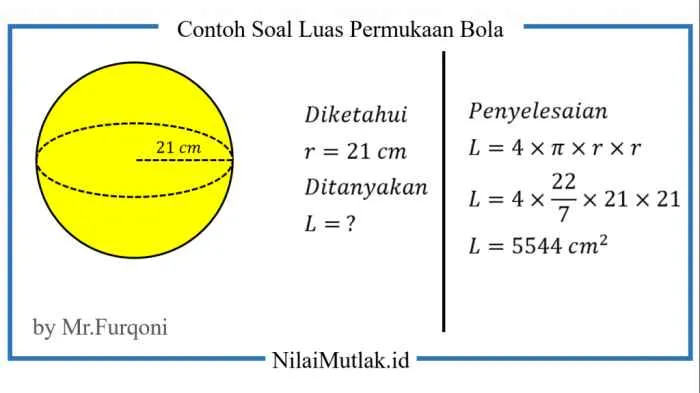
1. Sebuah bola memiliki luas permukaan 100π cm². Tentukan jari-jari bola tersebut.
2. Luas permukaan sebuah bola adalah 36π m². Berapakah diameter bola tersebut?

Penyelesaian:

1. Diketahui luas permukaan (L) = 100π cm². Kita gunakan rumus L = 4πr². Substitusikan nilai L: 100π = 4πr². Sederhanakan persamaan: 25 = r². Akar kuadrat kedua ruas: r = 5 cm. Jadi, jari-jari bola adalah 5 cm.
2. Diketahui luas permukaan (L) = 36π m². Kita gunakan rumus L = 4πr². Substitusikan nilai L: 36π = 4πr². Sederhanakan persamaan: 9 = r². Akar kuadrat kedua ruas: r = 3 m. Karena diameter (d) = 2r, maka diameter bola adalah 2 x 3 m = 6 m.

Tips dan Trik Menyelesaikan Soal Luas Permukaan Bola

Pastikan Anda memahami konsep dasar jari-jari dan diameter. Ingat bahwa diameter selalu dua kali lipat dari jari-jari. Sebelum melakukan perhitungan, selalu tuliskan rumus dan substitusikan nilai yang diketahui. Periksa kembali satuan yang digunakan dan pastikan konsistensi satuan sepanjang perhitungan. Jika luas permukaan diberikan dalam bentuk π, seringkali akan memudahkan perhitungan jika π dibiarkan tetap dalam persamaan hingga langkah akhir.

Kesalahan Umum dan Solusinya

Kesalahan umum yang sering terjadi adalah kesalahan dalam substitusi nilai ke dalam rumus atau kesalahan dalam operasi matematika dasar. Kesalahan lain yang sering terjadi adalah tidak memperhatikan satuan yang digunakan.

• Kesalahan: Salah dalam mensubstitusikan nilai luas permukaan atau keliru dalam melakukan operasi aljabar.
• Solusi: Periksa kembali langkah-langkah perhitungan secara teliti. Gunakan kalkulator jika diperlukan dan pastikan untuk mengecek kembali hasil akhir.
• Kesalahan: Tidak memperhatikan konsistensi satuan, misalnya mencampur satuan cm dan m dalam satu perhitungan.
• Solusi: Ubah semua satuan ke dalam satu sistem satuan yang sama sebelum melakukan perhitungan. Misalnya, ubah semua satuan ke cm atau m.

Pentingnya Memahami Konsep Dasar Geometri

Pemahaman yang kuat tentang konsep dasar geometri, seperti definisi bola, jari-jari, dan diameter, sangat krusial sebelum mempelajari rumus luas permukaan bola. Tanpa pemahaman konseptual yang kokoh, aplikasi rumus akan menjadi mekanis dan rentan terhadap kesalahan. Visualisasi bentuk geometri tiga dimensi juga membantu dalam memahami dan memecahkan masalah yang berkaitan dengan luas permukaan bola.

Pemungkas

Memahami cara menemukan rumus luas permukaan bola membuka pintu menuju pemahaman yang lebih dalam tentang geometri dan aplikasinya. Dari perhitungan sederhana hingga permasalahan yang lebih kompleks, penguasaan rumus ini menjadi bekal penting dalam berbagai bidang, mulai dari arsitektur hingga ilmu antariksa. Kemampuan untuk menghitung luas permukaan bola bukan hanya soal angka, tetapi juga kemampuan untuk memecahkan masalah dan mengaplikasikan pengetahuan matematis dalam konteks nyata.