Cara Menemukan Volume Bola Panduan Lengkap

Bola, bentuk geometris yang sederhana namun elegan, menyimpan rahasia perhitungan volume yang menarik. Dari perencanaan pembangunan stadion raksasa hingga perhitungan kapasitas tangki air, memahami cara menghitung volume bola menjadi kunci dalam berbagai bidang. Artikel ini akan mengupas tuntas rumus, penerapan, dan potensi kesalahan dalam perhitungan volume bola, dilengkapi contoh praktis dan ilustrasi yang mudah dipahami.

Menguasai perhitungan volume bola bukan sekadar soal rumus matematika; ini adalah kunci untuk memecahkan berbagai permasalahan di dunia nyata. Dengan pemahaman yang mendalam, Anda dapat mengaplikasikannya dalam berbagai konteks, mulai dari proyek teknik sipil berskala besar hingga perencanaan sederhana di kehidupan sehari-hari. Mari kita selami dunia menarik di balik perhitungan volume bola.

Rumus Volume Bola

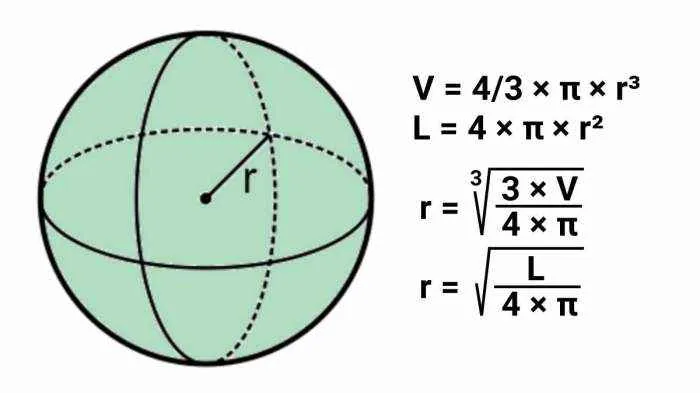
Menghitung volume bola merupakan konsep dasar dalam geometri. Pemahaman tentang rumus volume bola dan penerapannya penting dalam berbagai bidang, mulai dari ilmu fisika dan teknik hingga arsitektur dan desain. Artikel ini akan membahas secara detail rumus volume bola, langkah-langkah perhitungannya, serta beberapa contoh penerapannya.

Rumus dan Variabel

Rumus untuk menghitung volume bola adalah:

V = (4/3)πr³

di mana:

• V mewakili volume bola.
• r mewakili jari-jari bola.
• π (pi) adalah konstanta matematika dengan nilai pendekatan 3.14159.

Rumus ini menunjukkan bahwa volume bola berbanding lurus dengan pangkat tiga jari-jarinya. Artinya, jika jari-jari bola digandakan, volumenya akan meningkat delapan kali lipat.

Contoh Perhitungan: Jari-jari 5 cm

Mari kita hitung volume bola dengan jari-jari 5 cm. Berikut langkah-langkahnya:

1. Substitusikan nilai r = 5 cm ke dalam rumus: V = (4/3)π(5 cm)³
2. Hitung pangkat tiga jari-jari: (5 cm)³ = 125 cm³
3. Kalikan dengan (4/3)π: V = (4/3) * 3.14159 * 125 cm³
4. Hasil perhitungan: V ≈ 523.6 cm³

Jadi, volume bola dengan jari-jari 5 cm adalah sekitar 523.6 cm³.

Contoh Perhitungan dengan Jari-jari Berbeda

Berikut tabel yang menunjukkan perhitungan volume bola dengan jari-jari berbeda:

Jari-jari (cm)	Perhitungan	Volume (cm³)
2	(4/3)π(2)³	≈ 33.51
5	(4/3)π(5)³	≈ 523.60
10	(4/3)π(10)³	≈ 4188.79

Langkah-langkah Perhitungan Sistematis

Untuk menghitung volume bola, ikuti langkah-langkah berikut:

• Tentukan jari-jari bola (r).
• Pangkat tiga jari-jari (r³).
• Kalikan hasil pangkat tiga dengan (4/3)π.
• Hasil akhir adalah volume bola (V).

Penurunan Rumus dari Integral

Rumus volume bola dapat diturunkan menggunakan kalkulus integral. Dengan menggunakan metode integrasi kulit bola, kita dapat mengintegrasikan luas permukaan bola yang tak terhingga banyaknya untuk memperoleh volume totalnya. Proses ini melibatkan integrasi dari 0 hingga r terhadap variabel jari-jari, menghasilkan rumus V = (4/3)πr³.

Secara visual, bayangkan bola diiris menjadi lapisan-lapisan tipis yang sangat kecil. Luas setiap lapisan dikalikan dengan ketebalannya, kemudian dijumlahkan (diintegralkan) untuk mendapatkan volume total bola. Proses ini membutuhkan pemahaman mendalam tentang kalkulus integral dan di luar cakupan penjelasan ringkas ini.

Penerapan Rumus Volume Bola dalam Berbagai Konteks

Rumus volume bola, 4/3πr³, jauh lebih dari sekadar rumus matematika abstrak. Ia memiliki aplikasi praktis yang luas di berbagai bidang, dari perencanaan infrastruktur hingga industri manufaktur. Pemahaman mendalam tentang rumus ini memungkinkan kita untuk menyelesaikan berbagai permasalahan yang melibatkan objek berbentuk bola atau pendekatan bola.

Berikut ini beberapa contoh penerapan rumus volume bola dalam konteks kehidupan sehari-hari dan profesional, disertai penjelasan langkah penyelesaian dan implikasinya di berbagai sektor.

Contoh Soal Cerita dan Penyelesaiannya

Untuk memperjelas penerapan rumus volume bola, mari kita tinjau tiga contoh kasus yang relevan dengan kehidupan sehari-hari. Setiap kasus akan diuraikan langkah demi langkah untuk memudahkan pemahaman.

1. Soal 1: Sebuah balon udara berbentuk bola memiliki jari-jari 5 meter. Berapa volume udara di dalam balon tersebut?
2. Penyelesaian:
   1. Diketahui: r = 5 meter
   2. Rumus: V = 4/3πr³
   3. Substitusi: V = 4/3 * π * (5)³ = 523,6 meter kubik (dibulatkan)
   4. Jadi, volume udara di dalam balon adalah sekitar 523,6 meter kubik.
3. Soal 2: Sebuah toko roti membuat kue bolu berbentuk setengah bola dengan diameter 12 cm. Berapa volume kue bolu tersebut?
4. Penyelesaian:
   1. Diketahui: d = 12 cm, maka r = 6 cm
   2. Rumus: V = (1/2) * (4/3)πr³ (karena setengah bola)
   3. Substitusi: V = (1/2) * (4/3) * π * (6)³ = 452,39 cm kubik (dibulatkan)
   4. Jadi, volume kue bolu tersebut adalah sekitar 452,39 cm kubik.
5. Soal 3: Sebuah tangki pelampung bola di pelabuhan memiliki diameter 2 meter. Berapa kapasitas tangki tersebut?
6. Penyelesaian:
   1. Diketahui: d = 2 meter, maka r = 1 meter
   2. Rumus: V = (4/3)πr³
   3. Substitusi: V = (4/3) * π * (1)³ = 4,19 meter kubik (dibulatkan)
   4. Jadi, kapasitas tangki pelampung tersebut adalah sekitar 4,19 meter kubik.

Penggunaan Rumus Volume Bola dalam Teknik Sipil

Rumus volume bola krusial dalam perencanaan dan pembangunan infrastruktur. Misalnya, dalam perancangan saluran pembuangan bawah tanah berbentuk bola, perhitungan volume memastikan kapasitas aliran yang memadai. Selain itu, dalam desain kubah atau struktur bangunan berbentuk bola, perhitungan volume membantu menentukan jumlah material yang dibutuhkan dan stabilitas struktur. Ketelitian perhitungan volume sangat penting untuk menghindari kesalahan konstruksi dan memastikan keamanan.

Perhitungan Kapasitas Tangki Air Berbentuk Bola

Perhitungan kapasitas tangki air berbentuk bola sangat bergantung pada rumus volume bola. Setelah menentukan jari-jari tangki, rumus tersebut langsung dapat digunakan untuk menghitung volume air maksimal yang dapat ditampung. Hasil perhitungan ini penting untuk menentukan kebutuhan air, perencanaan sistem penyiraman, dan manajemen sumber daya air secara efisien. Sebagai contoh, tangki air berbentuk bola dengan jari-jari 1,5 meter memiliki kapasitas sekitar 14,14 meter kubik (4/3 * π * (1,5)³).

Bidang Studi dan Profesi yang Menggunakan Perhitungan Volume Bola

• Teknik Sipil: Seperti telah dijelaskan sebelumnya, perhitungan volume bola penting dalam perencanaan dan pembangunan infrastruktur.
• Teknik Kimia: Dalam desain reaktor kimia berbentuk bola, perhitungan volume sangat penting untuk menentukan efisiensi reaksi dan kapasitas produksi.
• Meteorologi: Perhitungan volume awan atau partikel atmosfer yang diasumsikan berbentuk bola digunakan dalam pemodelan cuaca dan iklim.

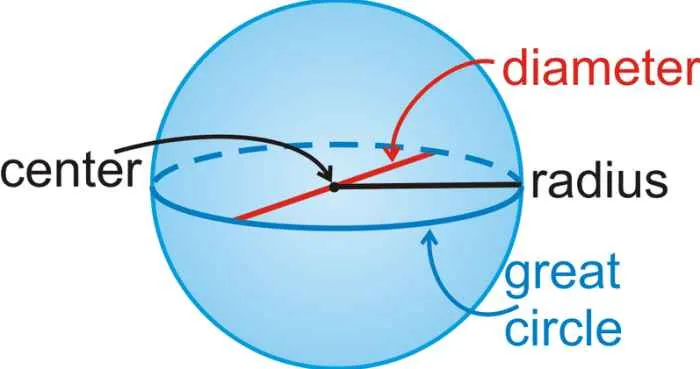
Menentukan Jari-jari Bola untuk Menghitung Volume

Menghitung volume bola membutuhkan pengetahuan tentang jari-jari (r) bola tersebut. Namun, terkadang informasi yang tersedia bukan langsung berupa jari-jari, melainkan luas permukaan atau keliling lingkaran besar bola. Oleh karena itu, penting untuk memahami bagaimana menentukan jari-jari dari informasi lain sebelum menghitung volume.

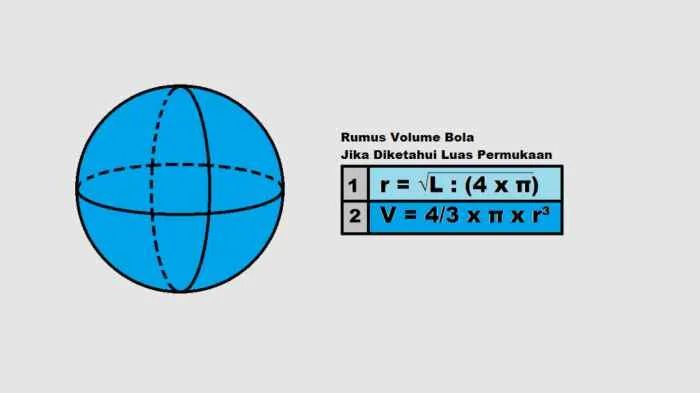
Menentukan Jari-jari dari Luas Permukaan

Luas permukaan bola dirumuskan sebagai 4πr². Jika luas permukaan (L) diketahui, maka jari-jari dapat dihitung dengan merumuskan ulang persamaan tersebut: r = √(L/(4π)). Setelah jari-jari ditemukan, kita dapat menghitung volume menggunakan rumus (4/3)πr³.

Contoh: Sebuah bola memiliki luas permukaan 100 cm². Untuk mencari volumenya, pertama-tama kita cari jari-jarinya:

r = √(100 cm² / (4π)) ≈ 2,82 cm

Kemudian, volume bola dapat dihitung:

V = (4/3)π(2,82 cm)³ ≈ 99,28 cm³

Menentukan Jari-jari dari Keliling Lingkaran Besar

Keliling lingkaran besar bola (K) sama dengan 2πr. Oleh karena itu, jari-jari dapat dihitung dengan rumus: r = K/(2π). Setelah jari-jari diketahui, volume bola dapat dihitung seperti biasa.

Pengukuran Jari-jari Bola Secara Praktis

Untuk mengukur jari-jari bola secara fisik, kita dapat menggunakan beberapa metode. Salah satu metode yang paling sederhana adalah dengan menggunakan jangka sorong atau mistar. Berikut langkah-langkahnya:

1. Letakkan bola pada permukaan datar yang stabil.
2. Letakkan jangka sorong atau mistar sehingga salah satu ujungnya menyentuh titik teratas bola dan ujung lainnya menyentuh permukaan datar di bawah bola. Ini akan memberikan diameter bola.
3. Bagi diameter yang terukur dengan dua untuk mendapatkan jari-jari bola.

Metode lain yang dapat digunakan adalah dengan menggunakan tali dan penggaris. Lingkarkan tali mengelilingi bola pada lingkaran besarnya, lalu ukur panjang tali tersebut. Bagi panjang tali dengan 2π untuk mendapatkan jari-jari.

Algoritma Perhitungan Volume Bola dari Diameter

Berikut algoritma langkah demi langkah untuk menghitung volume bola jika diketahui diameter (d):

1. Bagi diameter (d) dengan 2 untuk mendapatkan jari-jari (r): r = d/2
2. Pangkat jari-jari (r) pangkat tiga: r³
3. Kalikan hasil langkah 2 dengan (4/3)π: (4/3)πr³
4. Hasil dari langkah 3 adalah volume bola (V).

Pengaruh Kesalahan Pengukuran Jari-jari terhadap Volume

Kesalahan dalam pengukuran jari-jari akan berdampak signifikan pada hasil perhitungan volume bola. Karena rumus volume melibatkan pangkat tiga jari-jari (r³), kesalahan kecil dalam pengukuran jari-jari akan diperbesar secara kubik pada hasil akhir. Misalnya, kesalahan 1% dalam pengukuran jari-jari akan mengakibatkan kesalahan sekitar 3% pada perhitungan volume.

Sebagai ilustrasi, jika jari-jari sebenarnya adalah 5 cm dan terjadi kesalahan pengukuran sebesar 1 mm (0.1 cm), maka jari-jari yang terukur menjadi 5.1 cm. Volume bola dengan jari-jari 5 cm adalah (4/3)π(5)³ ≈ 523.6 cm³. Sementara volume bola dengan jari-jari 5.1 cm adalah (4/3)π(5.1)³ ≈ 557.5 cm³. Perbedaannya sekitar 6.4%, jauh lebih besar dari kesalahan pengukuran jari-jari (2%). Oleh karena itu, akurasi dalam pengukuran jari-jari sangat krusial untuk mendapatkan hasil perhitungan volume yang tepat.

Penggunaan Satuan dan Konversi Satuan dalam Perhitungan Volume Bola

Akurasi perhitungan volume bola sangat bergantung pada konsistensi satuan yang digunakan. Kesalahan kecil dalam satuan dapat berakibat pada perbedaan yang signifikan dalam hasil akhir, terutama dalam konteks aplikasi teknik atau ilmiah. Oleh karena itu, pemahaman yang mendalam tentang konversi satuan sangat krusial.

Pentingnya Konsistensi Satuan

Konsistensi satuan dalam perhitungan volume bola memastikan hasil yang akurat dan terhindar dari kesalahan perhitungan. Menggunakan campuran satuan (misalnya, jari-jari dalam sentimeter dan π tetap tanpa satuan) akan menghasilkan nilai volume yang salah. Seluruh perhitungan harus menggunakan satuan yang sama untuk menghindari ambiguitas dan memastikan hasil yang valid.

Contoh Perhitungan Volume Bola dengan Satuan Berbeda

Mari kita hitung volume bola dengan jari-jari 5 cm, 5 m, dan 5 km. Rumus volume bola adalah 4/3 πr³. Ingat, konsistensi satuan sangat penting.

Bola dengan jari-jari 5 cm:

Volume = (4/3) * π * (5 cm)³ ≈ 523,6 cm³

Bola dengan jari-jari 5 m:

Volume = (4/3) * π * (5 m)³ ≈ 523,6 m³

Bola dengan jari-jari 5 km:

Volume = (4/3) * π * (5 km)³ ≈ 523,6 km³

Perhatikan bahwa meskipun jari-jari hanya berbeda satuannya, volume yang dihasilkan juga memiliki satuan yang berbeda dan nilainya sangat berbeda pula. Konversi satuan diperlukan untuk membandingkan volume bola dengan ukuran yang berbeda.

Tabel Konversi Satuan Volume

Satuan	Ke cm³	Ke m³	Ke km³
cm³	1	1 x 10-6	1 x 10-15
m³	1 x 106	1	1 x 10-9
km³	1 x 1015	1 x 109	1

Pseudocode Konversi Satuan Volume

Berikut pseudocode sederhana untuk mengkonversi satuan volume bola:

INPUT volume_awal, satuan_awal, satuan_tujuan

IF satuan_awal == "cm³" AND satuan_tujuan == "m³" THEN
  volume_tujuan = volume_awal * 10^-6
ELSE IF satuan_awal == "cm³" AND satuan_tujuan == "km³" THEN
  volume_tujuan = volume_awal * 10^-15
ELSE IF satuan_awal == "m³" AND satuan_tujuan == "cm³" THEN
  volume_tujuan = volume_awal * 10^6
ELSE IF satuan_awal == "m³" AND satuan_tujuan == "km³" THEN
  volume_tujuan = volume_awal * 10^-9
ELSE IF satuan_awal == "km³" AND satuan_tujuan == "cm³" THEN
  volume_tujuan = volume_awal * 10^15
ELSE IF satuan_awal == "km³" AND satuan_tujuan == "m³" THEN
  volume_tujuan = volume_awal * 10^9
ELSE
  PRINT "Konversi satuan tidak didukung"
ENDIF

PRINT volume_tujuan, satuan_tujuan

Potensi Kesalahan Akibat Kesalahan Konversi Satuan

Kesalahan konversi satuan dapat mengakibatkan kesalahan perhitungan yang signifikan. Misalnya, kesalahan faktor 10⁶ dalam konversi antara m³ dan cm³ dapat menyebabkan perbedaan hasil hingga jutaan kali lipat. Hal ini dapat berdampak besar pada proyek konstruksi, perencanaan infrastruktur, atau penelitian ilmiah yang membutuhkan presisi tinggi. Oleh karena itu, selalu periksa kembali perhitungan dan pastikan konversi satuan dilakukan dengan benar.

Simpulan Akhir

Memahami cara menghitung volume bola membuka pintu menuju pemecahan masalah yang lebih kompleks di berbagai disiplin ilmu. Dari perhitungan sederhana hingga aplikasi rumit di bidang teknik, penguasaan konsep ini sangatlah penting. Dengan panduan praktis dan contoh-contoh yang diberikan, diharapkan pembaca dapat dengan percaya diri menerapkan rumus volume bola dalam berbagai situasi, dan menghindari kesalahan umum yang sering terjadi.