Cara Menentukan Volume Bola Panduan Lengkap

Bola, bentuk geometris yang sederhana namun menyimpan misteri perhitungan volume. Menguasai cara menentukan volume bola bukan sekadar soal rumus, melainkan kunci untuk memahami konsep ruang tiga dimensi dan penerapannya dalam berbagai bidang, dari arsitektur hingga astronomi. Bayangkan menghitung isi sebuah planet, atau mendesain tangki penyimpanan minyak bumi—semuanya berakar pada pemahaman mendasar tentang volume bola.

Artikel ini akan memandu Anda secara komprehensif, mulai dari rumus dasar hingga penerapannya dalam soal-soal cerita yang kompleks. Kita akan menjelajahi hubungan volume bola dengan luas permukaannya, membandingkannya dengan bangun ruang lain, dan bahkan menyingkap rahasia di balik perubahan volume akibat perubahan jari-jari. Siap untuk mengungkap rahasia di balik bola?

Rumus Volume Bola

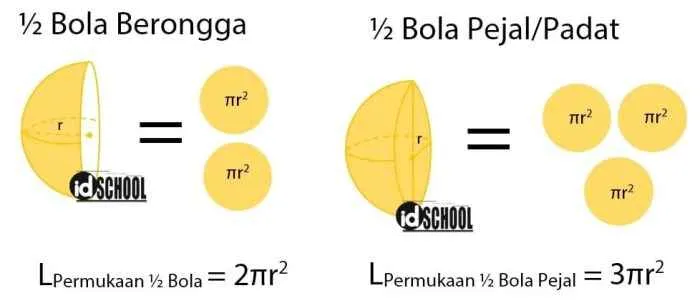
Menghitung volume bola merupakan konsep dasar dalam geometri yang memiliki aplikasi luas dalam berbagai bidang, mulai dari teknik sipil hingga astronomi. Memahami rumus dan penerapannya sangat penting untuk menyelesaikan berbagai permasalahan yang melibatkan objek berbentuk bola.

Rumus dan Variabel Volume Bola

Rumus untuk menghitung volume bola dinyatakan sebagai:

V = (4/3)πr³

di mana:

• V mewakili volume bola.
• r mewakili jari-jari bola.
• π (pi) adalah konstanta matematika, dengan nilai pendekatan 3.14159.

Rumus ini menunjukkan bahwa volume bola berbanding lurus dengan pangkat tiga dari jari-jarinya. Artinya, jika jari-jari bola dilipatgandakan, maka volumenya akan meningkat delapan kali lipat.

Contoh Perhitungan Volume Bola

Mari kita hitung volume bola dengan jari-jari 5 cm. Dengan menggunakan rumus di atas, kita substitusikan nilai r = 5 cm:

V = (4/3)π(5 cm)³ = (4/3)π(125 cm³) ≈ 523.6 cm³

Jelaskan Cara Menggiring Bola dalam Permainan Bola Basket

Jadi, volume bola dengan jari-jari 5 cm kira-kira 523.6 sentimeter kubik.

Tabel Rumus, Variabel, dan Satuan

Berikut tabel ringkasan yang menampilkan rumus volume bola, variabel yang terlibat, dan satuannya:

Besaran	Simbol	Satuan SI	Satuan Lain
Volume Bola	V	m³	cm³, liter, dll.
Jari-jari Bola	r	m	cm, mm, dll.
Pi (π)	π	–	–

Langkah-langkah Perhitungan Volume Bola

1. Tentukan nilai jari-jari (r) bola. Pastikan satuannya konsisten.
2. Substitusikan nilai r ke dalam rumus V = (4/3)πr³.
3. Hitung nilai πr³. Anda bisa menggunakan kalkulator atau nilai pendekatan π = 3.14159.
4. Kalikan hasil perhitungan langkah 3 dengan (4/3).
5. Tentukan satuan volume bola sesuai dengan satuan jari-jari yang digunakan.

Kondisi Khusus Jari-jari Bola

Jika jari-jari bola (r) bernilai nol (r = 0), maka volume bola juga akan bernilai nol (V = 0). Ini masuk akal karena bola dengan jari-jari nol tidak memiliki volume. Jika jari-jari bola bernilai negatif, hal ini tidak masuk akal dalam konteks geometri nyata karena jari-jari selalu merupakan besaran positif yang menunjukkan jarak dari pusat bola ke permukaannya. Oleh karena itu, nilai negatif untuk jari-jari tidak memiliki interpretasi fisik.

Penerapan Rumus Volume Bola dalam Berbagai Kasus

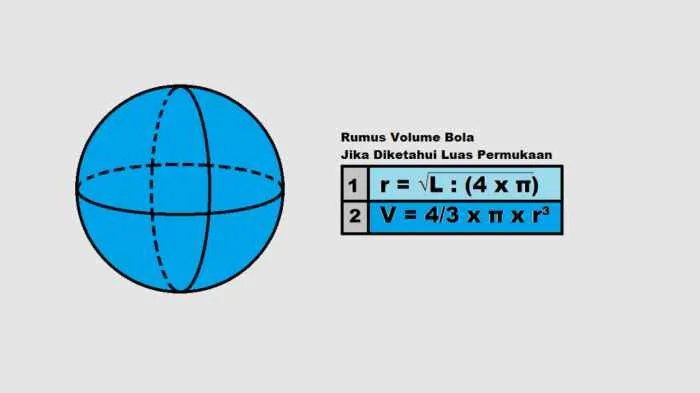
Setelah memahami rumus dasar volume bola, yaitu 4/3 πr³, penting untuk memahami penerapannya dalam berbagai skenario. Kemampuan menghitung volume bola memiliki aplikasi luas, mulai dari perencanaan konstruksi hingga perhitungan dalam bidang sains dan teknik.

Berikut beberapa contoh kasus yang akan mengilustrasikan bagaimana rumus volume bola diterapkan dalam pemecahan masalah.

Contoh Soal Cerita Perhitungan Volume Bola

Sebuah balon udara berbentuk bola memiliki jari-jari 7 meter. Berapa volume udara yang dapat ditampung balon tersebut? Gunakan nilai π = 22/7.

Penyelesaian: Kita gunakan rumus volume bola: V = 4/3 πr³. Dengan r = 7 meter dan π = 22/7, maka:

V = 4/3 x (22/7) x 7³ = 4/3 x (22/7) x 343 = 1437,33 meter kubik.

Jadi, balon udara tersebut dapat menampung sekitar 1437,33 meter kubik udara.

Mencari Jari-jari Bola jika Volume dan Nilai Phi Diketahui

Sebuah bola memiliki volume 113,04 cm³ dan nilai π = 3,14. Berapakah jari-jari bola tersebut?

Penyelesaian: Kita mulai dari rumus volume bola V = 4/3 πr³ dan kita ubah rumus tersebut untuk mencari r:

r³ = (3V)/(4π)

Tuliskan macam-macam cara melempar bola dalam permainan kasti

Substitusikan nilai V = 113,04 cm³ dan π = 3,14:

r³ = (3 x 113,04)/(4 x 3,14) = 27

r = ³√27 = 3 cm

Jadi, jari-jari bola tersebut adalah 3 cm.

Contoh Soal yang Melibatkan Konversi Satuan

Sebuah bola memiliki volume 5000 liter. Berapa volume bola tersebut dalam meter kubik? (Ingat: 1 liter = 0,001 meter kubik)

Penyelesaian: Konversikan liter ke meter kubik:

5000 liter x 0,001 m³/liter = 5 m³

Jadi, volume bola tersebut adalah 5 meter kubik.

Perhitungan Volume Setengah Bola

Untuk menghitung volume setengah bola, kita cukup membagi dua volume bola utuh. Misalnya, jika volume bola utuh adalah 1000 cm³, maka volume setengah bola adalah 500 cm³.

Rumusnya adalah:

V_{setengah bola} = (1/2) x (4/3)πr³ = (2/3)πr³

Perhitungan Volume Bola jika Diketahui Diameternya

Sebuah bola memiliki diameter 10 cm. Hitung volume bola tersebut. Gunakan π = 3,14.

Penyelesaian: Ingat bahwa jari-jari (r) adalah setengah dari diameter (d). Jadi, r = d/2 = 10 cm / 2 = 5 cm.

Kita gunakan rumus volume bola:

V = (4/3)πr³ = (4/3) x 3,14 x 5³ = 523,33 cm³

Jadi, volume bola tersebut adalah 523,33 cm³.

Hubungan Volume Bola dengan Luas Permukaan

Memahami hubungan antara volume dan luas permukaan bola krusial dalam berbagai aplikasi, mulai dari desain infrastruktur hingga perhitungan kapasitas penyimpanan. Rumus keduanya saling terkait erat, dan perubahan pada jari-jari akan berdampak signifikan pada keduanya. Pemahaman ini memungkinkan perhitungan yang lebih efisien dan akurat dalam berbagai konteks.

Rumus Volume dan Luas Permukaan Bola

Rumus volume bola adalah

V = (4/3)πr³

, di mana ‘r’ adalah jari-jari bola. Sementara rumus luas permukaan bola adalah

L = 4πr²

. Perhatikan bahwa keduanya bergantung pada jari-jari bola (r). Kuadrat jari-jari pada rumus luas permukaan menunjukkan bahwa perubahan jari-jari akan berdampak lebih besar pada luas permukaan dibandingkan pada volume.

Perhitungan Luas Permukaan dari Volume yang Diketahui

Jika volume bola diketahui, kita dapat menghitung jari-jarinya terlebih dahulu, lalu menggunakan jari-jari tersebut untuk menghitung luas permukaan. Misalnya, jika volume bola adalah 36π cm³, maka: (4/3)πr³ = 36π. Dengan menyelesaikan persamaan ini, kita dapatkan r = 3 cm. Selanjutnya, luas permukaannya adalah 4π(3)² = 36π cm².

Ilustrasi Hubungan Volume dan Luas Permukaan

Bayangkan sebuah balon. Saat kita menambah udara (meningkatkan volume), jari-jarinya membesar. Peningkatan jari-jari ini berdampak pada luas permukaan balon. Namun, peningkatan volume lebih signifikan dibandingkan peningkatan luas permukaan karena pangkat tiga pada rumus volume. Sebagai ilustrasi, jika jari-jari digandakan, volume akan meningkat delapan kali lipat (2³=8), sedangkan luas permukaan hanya meningkat empat kali lipat (2²=4).

Perbandingan dengan Bangun Ruang Lainnya

Bangun Ruang	Rumus Volume	Rumus Luas Permukaan
Kubus	s³	6s²
Tabung	πr²t	2πr(r+t)
Bola	(4/3)πr³	4πr²

Perbandingan ini menunjukkan bahwa rumus volume dan luas permukaan untuk setiap bangun ruang berbeda dan bergantung pada dimensi masing-masing bangun ruang. Bola memiliki rumus yang unik, melibatkan konstanta π (pi).

Contoh Soal Gabungan Volume dan Luas Permukaan

Sebuah bola memiliki luas permukaan 100π cm². Hitung volume bola tersebut. Penyelesaian: Dari rumus luas permukaan, 4πr² = 100π, maka r² = 25, dan r = 5 cm. Selanjutnya, volume bola adalah (4/3)π(5)³ = 500π/3 cm³.

Pemahaman Konsep Volume

Memahami konsep volume, khususnya volume bola, merupakan kunci untuk menyelesaikan berbagai permasalahan dalam geometri dan bidang terkait. Konsep ini tak hanya penting dalam konteks akademis, tetapi juga memiliki aplikasi praktis dalam berbagai industri, mulai dari konstruksi hingga farmasi. Bayangkan saja, perhitungan volume tangki penyimpanan minyak bumi, desain bola sepak, atau bahkan pembuatan pil obat—semuanya bergantung pada pemahaman yang tepat tentang volume bola.

Konsep Volume dan Aplikasinya pada Bola

Volume secara umum didefinisikan sebagai besaran ruang tiga dimensi yang ditempati oleh suatu benda. Dalam konteks bola, volume merepresentasikan jumlah ruang yang dipenuhi oleh bola tersebut. Analogi yang tepat adalah membayangkan bola diisi dengan air. Volume bola adalah jumlah air yang dibutuhkan untuk mengisi bola tersebut hingga penuh. Konsep ini penting karena memungkinkan kita untuk menghitung kapasitas suatu wadah berbentuk bola atau menentukan jumlah material yang dibutuhkan untuk membuat bola dengan ukuran tertentu.

Penjelasan Sederhana Volume Bola untuk Siswa SD

Volume bola adalah ukuran seberapa banyak ruang yang ditempati oleh bola. Bayangkan bola seperti balon yang ditiup. Semakin besar balon, semakin banyak udara di dalamnya, artinya semakin besar volumenya. Kita bisa menghitung volume bola menggunakan rumus tertentu yang melibatkan ukuran jari-jari bola.

Pengaruh Perubahan Jari-jari terhadap Volume Bola

Jari-jari bola memiliki hubungan yang sangat erat dengan volumenya. Rumus volume bola (4/3πr³) menunjukkan bahwa volume berbanding lurus dengan pangkat tiga jari-jari (r). Artinya, jika jari-jari bola dilipatgandakan, volumenya akan meningkat delapan kali lipat (2³ = 8). Sebaliknya, jika jari-jari dibagi dua, volumenya akan menjadi 1/8 dari volume semula. Perubahan kecil pada jari-jari akan berdampak signifikan pada volume, terutama pada bola dengan jari-jari yang besar.

Langkah Memahami Konsep Volume Bola Secara Bertahap

1. Mengerti definisi volume: Pahami dulu pengertian volume secara umum sebagai ruang tiga dimensi yang ditempati benda.
2. Visualisasi bola: Bayangkan bentuk bola dan bagaimana ruang tiga dimensi tersebut terisi.
3. Memahami jari-jari: Pahami pengertian jari-jari bola sebagai jarak dari pusat bola ke permukaannya.
4. Mempelajari rumus volume bola: Rumus V = (4/3)πr³ menghubungkan volume (V) dengan jari-jari (r).
5. Penerapan rumus: Latih penerapan rumus dengan berbagai contoh soal, mulai dari bola dengan jari-jari kecil hingga besar.
6. Menghubungkan dengan kehidupan nyata: Cari contoh aplikasi perhitungan volume bola dalam kehidupan sehari-hari, misalnya menghitung volume bola dunia atau volume tangki air berbentuk bola.

Ringkasan Penutup

Memahami cara menentukan volume bola membuka pintu menuju pemahaman yang lebih dalam tentang geometri ruang tiga dimensi. Dari perhitungan sederhana hingga aplikasi kompleks dalam berbagai disiplin ilmu, penguasaan konsep ini terbukti krusial. Dengan menguasai rumus, memahami hubungannya dengan luas permukaan, dan mampu menerapkannya dalam berbagai skenario, Anda telah memperluas kemampuan analitis dan pemecahan masalah Anda. Jadi, tak hanya sekadar angka, tetapi pemahaman yang mendalam tentang volume bola yang akan Anda bawa.