Cara Menghitung Volume Bola Panduan Lengkap

Bola, bentuk geometris yang sederhana namun elegan, menyimpan rahasia perhitungan volume yang menarik. Menguasai cara menghitung volume bola bukan hanya sekadar memahami rumus, tetapi juga membuka pintu untuk menyelesaikan berbagai permasalahan praktis, dari menghitung isi tangki penyimpanan hingga menganalisis volume sel darah merah. Mari kita selami dunia menarik perhitungan volume bola, mulai dari rumus dasar hingga aplikasi di kehidupan nyata.

Artikel ini akan memandu Anda secara komprehensif melalui proses menghitung volume bola, mulai dari pemahaman rumus dasar hingga aplikasi rumus tersebut dalam berbagai skenario. Kita akan menjelajahi contoh-contoh perhitungan, membahas hubungan volume bola dengan besaran lain seperti luas permukaan, dan bahkan membahas pendekatan untuk menghitung volume bola yang tidak beraturan. Siap untuk menguasai perhitungan volume bola?

Rumus Menghitung Volume Bola

Menghitung volume bola merupakan konsep dasar dalam geometri yang memiliki aplikasi luas di berbagai bidang, mulai dari teknik sipil hingga fisika. Memahami cara menghitungnya sangat penting untuk menyelesaikan berbagai permasalahan yang melibatkan bentuk tiga dimensi ini. Rumus yang digunakan sederhana namun efektif, memungkinkan kita untuk menentukan ruang yang ditempati oleh suatu bola dengan mudah.

Berikut ini akan dijelaskan secara detail rumus perhitungan volume bola, beserta contoh penerapannya dengan berbagai nilai jari-jari.

Rumus Umum Volume Bola

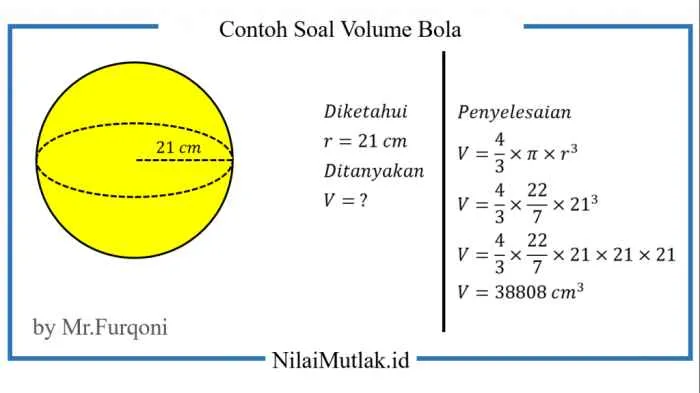
Rumus umum untuk menghitung volume bola (V) adalah:

V = (4/3)πr³

Jelaskan Cara Menangkap Bola dalam Permainan Bola Basket

di mana:

• V = Volume bola
• r = Jari-jari bola
• π (pi) ≈ 3.14159

Rumus ini menunjukkan bahwa volume bola berbanding lurus dengan pangkat tiga dari jari-jarinya. Artinya, jika jari-jari bola diperbesar dua kali lipat, maka volumenya akan menjadi delapan kali lipat.

Contoh Perhitungan Volume Bola

Berikut beberapa contoh perhitungan volume bola dengan jari-jari berbeda, yang akan disajikan dalam :

No	Jari-jari Bola (r)	Perhitungan Volume	Hasil Volume (satuan kubik)
1	5 cm	(4/3) x 3.14159 x 5³	523.60 cm³
2	10 cm	(4/3) x 3.14159 x 10³	4188.79 cm³
3	15 cm	(4/3) x 3.14159 x 15³	14137.17 cm³

Langkah Perhitungan Detail (Jari-jari 5 cm)

Berikut langkah-langkah perhitungan volume bola dengan jari-jari 5 cm:

1. Substitusikan nilai jari-jari (r = 5 cm) ke dalam rumus: V = (4/3)πr³
2. V = (4/3) x 3.14159 x 5³
3. V = (4/3) x 3.14159 x 125
4. V = 523.60 cm³

Menggunakan Diameter Bola

Jika yang diketahui adalah diameter (d) bola, bukan jari-jari, maka rumus dapat dimodifikasi. Ingat bahwa jari-jari adalah setengah dari diameter (r = d/2). Dengan demikian, rumus volume bola dapat ditulis sebagai:

V = (1/6)πd³

Cara Menangkap Bola Basket yang Benar Adalah Kunci Kemenangan

Dengan menggunakan rumus ini, kita dapat langsung menghitung volume bola jika diameternya diketahui, tanpa perlu menghitung jari-jari terlebih dahulu. Penggunaan rumus ini akan memberikan hasil yang sama dengan rumus sebelumnya.

Penerapan Rumus dalam Berbagai Kasus

Memahami rumus volume bola, 4/3πr³, bukan hanya sekadar menghafal rumus matematika. Penerapannya sangat luas, mulai dari perencanaan konstruksi hingga analisis data dalam berbagai bidang. Berikut beberapa contoh penerapan rumus volume bola dalam kasus nyata.

Contoh Soal Cerita dan Penyelesaiannya

Sebuah bola kasti memiliki diameter 10 cm. Berapakah volume bola kasti tersebut?

1. Identifikasi variabel: Diameter (d) = 10 cm. Jari-jari (r) = d/2 = 5 cm. π ≈ 3,14
2. Tentukan rumus: Volume bola (V) = 4/3πr³
3. Substitusi nilai: V = (4/3) x 3,14 x (5 cm)³
4. Hitung volume: V = (4/3) x 3,14 x 125 cm³ = 523,33 cm³
5. Kesimpulan: Volume bola kasti tersebut adalah sekitar 523,33 cm³.

Contoh Soal Cerita Lain: Volume Bola dalam Desain Interior

Seorang desainer interior merencanakan sebuah lampu hias berbentuk setengah bola dengan diameter 30 cm. Berapa volume kaca yang dibutuhkan untuk membuat lampu hias tersebut?

1. Variabel: Diameter (d) = 30 cm; Jari-jari (r) = d/2 = 15 cm; π ≈ 3,14
2. Rumus: Volume setengah bola = (1/2) x (4/3)πr³
3. Substitusi dan perhitungan: Volume = (1/2) x (4/3) x 3,14 x (15 cm)³ = 5652 cm³
4. Kesimpulan: Desainer membutuhkan sekitar 5652 cm³ kaca untuk membuat lampu hias tersebut.

Pentingnya memahami rumus volume bola tidak hanya terbatas pada soal-soal matematika. Dalam kehidupan sehari-hari, pemahaman ini dapat membantu dalam berbagai hal, mulai dari menghitung kapasitas tangki air berbentuk bola, menentukan jumlah material yang dibutuhkan untuk membuat objek berbentuk bola, hingga dalam perencanaan dan desain arsitektur.

Hubungan Volume Bola dengan Besaran Lain

Memahami volume bola tak cukup hanya dengan mengetahui rumusnya. Pemahaman yang lebih komprehensif mencakup bagaimana volume ini berelasi dengan besaran lain, terutama luas permukaan bola. Hubungan ini penting dalam berbagai aplikasi, mulai dari perencanaan konstruksi hingga perhitungan dalam fisika dan teknik.

Mengetahui hubungan antara volume dan luas permukaan memungkinkan kita untuk melakukan perhitungan yang lebih efisien dan menyeluruh. Misalnya, dalam desain wadah berbentuk bola, mengetahui luas permukaan membantu menentukan material yang dibutuhkan, sementara volume menentukan kapasitas wadah tersebut. Berikut penjelasan lebih detail mengenai hubungan tersebut.

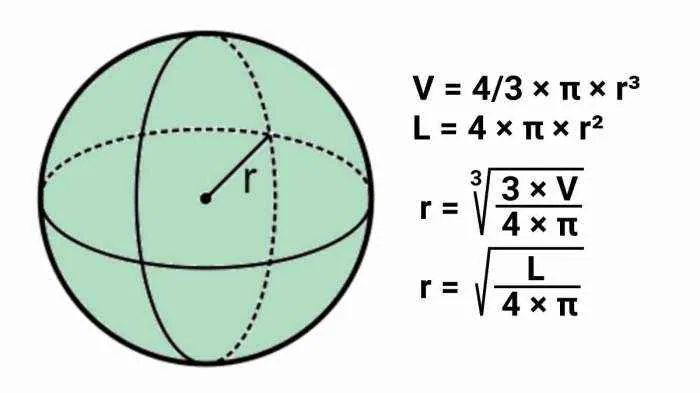
Luas Permukaan dan Volume Bola

Rumus luas permukaan bola adalah 4πr², di mana ‘r’ adalah jari-jari bola. Rumus volume bola sendiri adalah (4/3)πr³. Perhatikan bahwa kedua rumus ini memiliki variabel yang sama, yaitu jari-jari (r). Ini menunjukkan hubungan langsung antara luas permukaan dan volume bola; keduanya bergantung secara kuadratik dan kubik terhadap jari-jari, masing-masing.

Dengan demikian, jika jari-jari bola meningkat, baik luas permukaan maupun volumenya akan meningkat. Namun, peningkatan volume akan lebih signifikan daripada peningkatan luas permukaan karena hubungan kubik terhadap jari-jari. Hal ini dapat diilustrasikan dengan membandingkan rasio perubahan volume terhadap perubahan luas permukaan ketika jari-jari bola ditingkatkan.

Mengubah Rumus Volume jika Diketahui Luas Permukaan

Jika luas permukaan (L) diketahui, kita dapat menentukan jari-jari bola dengan rumus r = √(L/4π). Nilai ‘r’ ini kemudian dapat disubstitusikan ke dalam rumus volume bola, menghasilkan rumus volume bola dalam fungsi luas permukaan: V = (1/3)√(L³/64π²).

Dengan rumus ini, kita dapat langsung menghitung volume bola tanpa perlu menghitung jari-jari terlebih dahulu. Ini memberikan efisiensi dalam perhitungan, terutama jika luas permukaan bola sudah diketahui.

Ilustrasi Hubungan Volume dan Jari-jari Bola

Bayangkan dua bola, Bola A dan Bola B. Misalkan Bola A memiliki jari-jari 1 cm, sementara Bola B memiliki jari-jari 2 cm. Volume Bola A adalah (4/3)π(1)³ = (4/3)π cm³, sedangkan volume Bola B adalah (4/3)π(2)³ = (32/3)π cm³. Perhatikan bahwa meskipun jari-jari Bola B hanya dua kali lipat jari-jari Bola A, volumenya menjadi delapan kali lipat (32/3)π / (4/3)π = 8.

Ilustrasi ini menunjukkan bagaimana peningkatan jari-jari bola secara linear akan mengakibatkan peningkatan volume bola secara kubik. Semakin besar jari-jari, semakin signifikan peningkatan volumenya relatif terhadap peningkatan jari-jari.

Menghitung Jari-jari Bola jika Diketahui Volumenya

1. Tuliskan rumus volume bola: V = (4/3)πr³
2. Susun ulang rumus untuk mencari jari-jari: r = ³√[(3V)/(4π)]
3. Substitusikan nilai volume (V) yang diketahui ke dalam rumus.
4. Hitung nilai r untuk mendapatkan jari-jari bola.

Dengan mengikuti langkah-langkah ini, kita dapat dengan mudah menghitung jari-jari bola jika volumenya sudah diketahui. Proses ini merupakan kebalikan dari menghitung volume jika jari-jari diketahui.

Menghitung Volume Bola yang Tidak Beraturan

Rumus 4/3πr³ hanya berlaku sempurna untuk bola dengan bentuk ideal. Namun, dalam dunia nyata, kita seringkali berhadapan dengan objek yang menyerupai bola namun memiliki penyimpangan bentuk, misalnya bola yang sedikit penyok atau tidak sepenuhnya bulat sempurna. Menghitung volume benda-benda tersebut membutuhkan pendekatan yang berbeda, mengandalkan metode perkiraan untuk mencapai hasil yang cukup akurat.

Metode perkiraan volume bola tidak beraturan umumnya melibatkan pemodelan bentuk objek tersebut dan perhitungan volume berdasarkan model tersebut. Akurasi hasil sangat bergantung pada seberapa baik model merepresentasikan bentuk objek sebenarnya.

Metode Perkiraan Volume Bola Tidak Beraturan

Salah satu metode yang dapat digunakan adalah dengan membagi bola tidak beraturan menjadi beberapa bagian kecil yang mendekati bentuk geometris sederhana, seperti kubus atau prisma. Volume masing-masing bagian dihitung, kemudian dijumlahkan untuk mendapatkan perkiraan total volume bola tidak beraturan. Semakin kecil bagian-bagian tersebut, semakin akurat perkiraannya. Metode lain melibatkan penggunaan teknik integrasi numerik, tetapi metode ini memerlukan pemahaman kalkulus dan perangkat lunak khusus.

Ilustrasi Metode Perkiraan

Bayangkan sebuah bola basket yang sedikit penyok di satu sisi. Kita dapat memperkirakan volumenya dengan membayangkan bola tersebut dibagi menjadi beberapa irisan tipis berbentuk silinder. Kita ukur jari-jari setiap irisan di beberapa titik sepanjang ketinggiannya. Dengan menggunakan rumus volume silinder (πr²h), kita dapat menghitung volume setiap irisan. Jumlah volume semua irisan akan memberikan perkiraan volume bola basket yang penyok tersebut. Semakin banyak irisan yang kita buat, semakin akurat perkiraan volumenya.

Algoritma Perkiraan Volume

Berikut algoritma sederhana untuk menghitung perkiraan volume bola tidak beraturan menggunakan metode irisan silinder:

1. Bagi bola tidak beraturan menjadi N irisan silinder dengan tinggi h.
2. Ukur jari-jari (r_i) setiap irisan di beberapa titik sepanjang ketinggiannya (i = 1, 2, …, N).
3. Hitung volume setiap irisan menggunakan rumus: V_i = πr_i²h.
4. Jumlahkan volume semua irisan: V_total = ΣV_i (i = 1 sampai N).

Perlu diingat bahwa akurasi hasil bergantung pada jumlah irisan (N) dan akurasi pengukuran jari-jari setiap irisan.

Perbandingan Volume Bola Sempurna dan Tidak Beraturan

Jenis Bola	Jari-jari (cm)	Volume (cm³)	Penyimpangan (%)
Bola Sempurna	10	4188.79	–
Bola Tidak Beraturan (Contoh)	10 (rata-rata)	3900 (perkiraan)	~7%

Tabel di atas menunjukkan perbandingan volume bola sempurna dengan jari-jari 10 cm dan bola tidak beraturan dengan jari-jari rata-rata 10 cm. Perbedaan volume menunjukkan penyimpangan yang terjadi akibat ketidaksempurnaan bentuk bola. Angka 3900 cm³ merupakan perkiraan dan dapat berbeda tergantung pada metode dan akurasi pengukuran yang digunakan.

Simpulan Akhir

Memahami cara menghitung volume bola merupakan kunci untuk memecahkan berbagai permasalahan di berbagai bidang, mulai dari ilmu pengetahuan hingga rekayasa. Kemampuan untuk mengaplikasikan rumus volume bola, bahkan untuk objek yang tidak sepenuhnya sempurna, menunjukkan pemahaman konseptual yang kuat. Dengan pemahaman yang mendalam ini, Anda siap menghadapi tantangan perhitungan volume yang lebih kompleks dan menerapkannya dalam kehidupan sehari-hari.